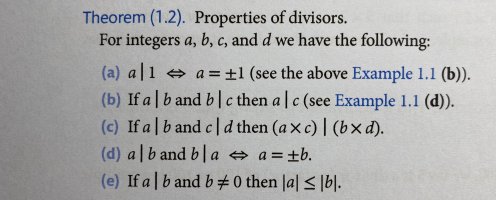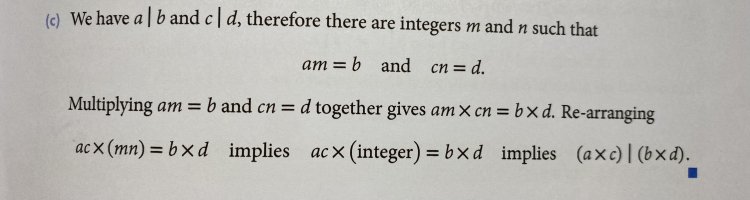Divisibility Proof

[jpanknin]

I'm self-studying through a number theory book (Singh - Number Theory Step by Step) and I'm having trouble with one of the proofs.

The statement is [imath] If \:(\: a\: | \:b\:) \:and \:( \:c \:| \:d\:) \:then \:(\:ac\:) \:| \:(\: bd\:)[/imath].

I set [imath]\:ax \: = \: b[/imath] and [imath]cy \: = \: d[/imath] for some integers [imath]x, \:y[/imath].

Then substituting [imath]ax[/imath] for [imath]b[/imath] and [imath]cy[/imath] for [imath]d[/imath], I end up with [imath](\: ac \:) | (\:axcy\:)[/imath]. Rearranging I get [imath](\:ac \:) | (\: acxy)[/imath] and [imath](\:ac \:) | (\: ac(xy))[/imath] where [imath]x \times y[/imath] is an integer because x and y are integers.

Dividing both sides by [imath](\:ac \:)[/imath] gives [imath]1\: | (\: xy)[/imath].

The book proceeds differently by [imath](\:ax \times cy \:) | (\: bd \:))[/imath] and [imath](\:ac \times xy \:) | (\: bd \:))[/imath] where xy is the integer.

I know the book method works, but if I were to proceed using my method, where did I go wrong to end up with [imath]1\: | (\: xy)[/imath]?

 

[blamocur]

If [imath]ax=b[/imath] and [imath]cy=d[/imath] then [imath](ac)(xy) = (bd)[/imath], which means [imath](ac)|(bd)[/imath].

 

[Dr.Peterson]

Then substituting [imath]ax[/imath] for [imath]b[/imath] and [imath]cy[/imath] for [imath]d[/imath], I end up with [imath](\: ac \:) | (\:axcy\:)[/imath]. Rearranging I get [imath](\:ac \:) | (\: acxy)[/imath] and [imath](\:ac \:) | (\: ac(xy))[/imath] where [imath]x \times y[/imath] is an integer because x and y are integers.

Dividing both sides by [imath](\:ac \:)[/imath] gives [imath]1\: | (\: xy)[/imath].

where did I go wrong to end up with [imath]1\: | (\: xy)[/imath]?

When you write a proof, you must do only things that are known to be valid -- that is, each step must be supported by a previously proved theorem.

Can you quote a theorem that says you can "divide both sides" of a divisibility statement?

 

[jpanknin]

If [imath]ax=b[/imath] and [imath]cy=d[/imath] then [imath](ac)(xy) = (bd)[/imath], which means [imath](ac)|(bd)[/imath].

Yes, this is what I'm trying to prove, but somehow I ended up with the xy on the wrong side. It should be on the left and I got it on the right.

 

[jpanknin]

When you write a proof, you must do only things that are known to be valid -- that is, each step must be supported by a previously proved theorem.

Can you quote a theorem that says you can "divide both sides" of a divisibility statement?

Well, if I think about this as a fraction [imath]\frac{y}{x}[/imath] where x | y and x and y have a common denominator, then it could be reduced by dividing both terms by that common denominator (even if the gcd = 1 then it would just stay the same, but would still be divisible by 1). In the proof we ASSUME that x | y is true, so both terms should be divisible by a common denominator.

 

[fresh_42]

Yes, this is what I'm trying to prove, but somehow I ended up with the xy on the wrong side.

You should avoid divisions by all means in number theory! A quotient [imath] q=\dfrac{a}{b} [/imath] should always be written as [imath]q\cdot b = a [/imath] or [imath] q\,|\,a [/imath] or [imath] b\,|\,a [/imath] or using the modulo function [imath] a\equiv 0\pmod{q} [/imath] or [imath] a\equiv 0\pmod{b} [/imath] and if you still cannot avoid quotients, then write [imath] q=ab^{-1} [/imath] which is automatically an equation in [imath] \mathbb{Q} [/imath] and not in [imath] \mathbb{Z} [/imath] anymore since the integers do not have any divisions! That's why divisibility is a question hosted in the ring of integers as a very special case, and not as a question in the field of rational numbers where it is standard for any number (different from zero). And if we are in [imath] \mathbb{Z} [/imath] with our question then we should not use divisions and quotients!

The alternative to divisions of integers is the Euclidean algorithm. We write [imath] a=q\cdot b+r [/imath] with [imath] 0 \leq r<b [/imath] for any two numbers [imath] a,b [/imath] that we want to divide. Again an equation without using a division.

 

[jpanknin]

You should avoid divisions by all means in number theory! A quotient [imath] q=\dfrac{a}{b} [/imath] should always be written as [imath]q\cdot b = a [/imath] or [imath] q\,|\,a [/imath] or [imath] b\,|\,a [/imath] or using the modulo function [imath] a\equiv 0\pmod{q} [/imath] or [imath] a\equiv 0\pmod{b} [/imath] and if you still cannot avoid quotients, then write [imath] q=ab^{-1} [/imath] which is automatically an equation in [imath] \mathbb{Q} [/imath] and not in [imath] \mathbb{Z} [/imath] anymore since the integers do not have any divisions! That's why divisibility is a question hosted in the ring of integers as a very special case, and not as a question in the field of rational numbers where it is standard for any number (different from zero). And if we are in [imath] \mathbb{Z} [/imath] with our question then we should not use divisions and quotients!

The alternative to divisions of integers is the Euclidean algorithm. We write [imath] a=q\cdot b+r [/imath] with [imath] 0 \leq r<b [/imath] for any two numbers [imath] a,b [/imath] that we want to divide. Again an equation without using a division.

I've not studied fields or rings and this book is not yet at modular arithmetic, so we should be able to solve this with the basic divisibility properties we've covered to this point.

 

[Dr.Peterson]

Well, if I think about this as a fraction [imath]\frac{y}{x}[/imath] where x | y and x and y have a common denominator, then it could be reduced by dividing both terms by that common denominator (even if the gcd = 1 then it would just stay the same, but would still be divisible by 1). In the proof we ASSUME that x | y is true, so both terms should be divisible by a common denominator.

I'll repeat: Were you taught a theorem that says you can do this? If so, then you can apply that theorem. If not, you can't just assume it by analogy. (Of course, you could try to actually prove it, and then use it. And you've come close to doing that.)

But then, there's another question: Is what you want to do useful? This is important in writing proofs: You must not only do valid things, but specifically do things that lead toward the goal. Did you notice that your conclusion, that 1 | (xy), is always true, for any values of the variables? That means that what you proved isn't wrong; it just isn't what you wanted!

Let's look at your steps:

The statement is [imath] \text{If }\:(\: a\: | \:b\:) \:\text{and }\:( \:c \:| \:d\:) \:\text{then }\:(\:ac\:) \:| \:(\: bd\:)[/imath].

I set [imath]\:ax \: = \: b[/imath] and [imath]cy \: = \: d[/imath] for some integers [imath]x, \:y[/imath].

This is a good start.

Then substituting [imath]ax[/imath] for [imath]b[/imath] and [imath]cy[/imath] for [imath]d[/imath], I end up with [imath](\: ac \:) | (\:axcy\:)[/imath]. Rearranging I get [imath](\:ac \:) | (\: acxy)[/imath] and [imath](\:ac \:) | (\: ac(xy))[/imath] where [imath]x \times y[/imath] is an integer because x and y are integers.

You can't substitute in the fact you are trying to prove! You don't yet know that it is true!

Possibly what you meant is that the goal is equivalent to showing that ac divides (ax)(cy). And that is easy to show to be true!

But instead, you are in fact assuming that this is true, and then continuing ...

Dividing both sides by [imath](\:ac \:)[/imath] gives [imath]1\: | (\: xy)[/imath].

This is simply the wrong direction to go. You are starting from the conclusion, rather than from the givens, and that is the wrong direction for a proof.

In writing a proof, you must always keep in mind what you know, and what you want to show,

The book proceeds differently by [imath](\:ax \times cy \:) | (\: bd \:))[/imath] and [imath](\:ac \times xy \:) | (\: bd \:))[/imath] where xy is the integer.

I know the book method works, but if I were to proceed using my method, where did I go wrong to end up with [imath]1\: | (\: xy)[/imath]?

Can you show their actual proof? I doubt this is really what they said.

I've not studied fields or rings and this book is not yet at modular arithmetic, so we should be able to solve this with the basic divisibility properties we've covered to this point.

Can you show us those properties?

 

[jpanknin]

I'll repeat: Were you taught a theorem that says you can do this? If so, then you can apply that theorem. If not, you can't just assume it by analogy. (Of course, you could try to actually prove it, and then use it. And you've come close to doing that.)

But then, there's another question: Is what you want to do useful? This is important in writing proofs: You must not only do valid things, but specifically do things that lead toward the goal. Did you notice that your conclusion, that 1 | (xy), is always true, for any values of the variables? That means that what you proved isn't wrong; it just isn't what you wanted!

Let's look at your steps:

This is a good start.

You can't substitute in the fact you are trying to prove! You don't yet know that it is true!

Possibly what you meant is that the goal is equivalent to showing that ac divides (ax)(cy). And that is easy to show to be true!

But instead, you are in fact assuming that this is true, and then continuing ...

This is simply the wrong direction to go. You are starting from the conclusion, rather than from the givens, and that is the wrong direction for a proof.

In writing a proof, you must always keep in mind what you know, and what you want to show,

Can you show their actual proof? I doubt this is really what they said.


Can you show us those properties?

See images below for properties covered thus far and the proof provided by the book.

 

[jpanknin]

I'll repeat: Were you taught a theorem that says you can do this? If so, then you can apply that theorem. If not, you can't just assume it by analogy. (Of course, you could try to actually prove it, and then use it. And you've come close to doing that.)

But then, there's another question: Is what you want to do useful? This is important in writing proofs: You must not only do valid things, but specifically do things that lead toward the goal. Did you notice that your conclusion, that 1 | (xy), is always true, for any values of the variables? That means that what you proved isn't wrong; it just isn't what you wanted!

Let's look at your steps:

This is a good start.

You can't substitute in the fact you are trying to prove! You don't yet know that it is true!

Possibly what you meant is that the goal is equivalent to showing that ac divides (ax)(cy). And that is easy to show to be true!

But instead, you are in fact assuming that this is true, and then continuing ...

This is simply the wrong direction to go. You are starting from the conclusion, rather than from the givens, and that is the wrong direction for a proof.

In writing a proof, you must always keep in mind what you know, and what you want to show,

Can you show their actual proof? I doubt this is really what they said.


Can you show us those properties?

What I've covered in proofs says that you ASSUME the hypothesis is true and proceed with that assumption. And by the definition of divisibility:

We say integer [imath]a \neq 0[/imath] divides integer b if and only if there exists an integer m such that [imath]a \times m = b[/imath].

So if we ASSUME the hypothesis is true and use the definition above, why can't you make the substitution for b and d?

 

[fresh_42]

I've not studied fields or rings and this book is not yet at modular arithmetic, so we should be able to solve this with the basic divisibility properties we've covered to this point.

Sure. Simply write equations [imath] q=\dfrac{a}{b} [/imath] as integer equations: [imath] q\cdot b=a. [/imath] That avoids mistakes by divisions.

You had been given [imath] a\,|\,b[/imath] and [imath] c\,|\,d .[/imath]

The first thing to ask is what that means! It means that there are integers [imath] x,y [/imath] such that [imath] ax=b\, , \,cy=d [/imath] as you correctly noted.

The crucial point was what has been said in post #2.
[imath] ax=b\wedge cy=d \Longrightarrow b\cdot d = (ax)\cdot (cy).[/imath]

<Here come some algebraic manipulations using the associativity and the commutativity of integer multiplication.>

Then we get [imath] (ac)\cdot z = bd [/imath] for some integer [imath] z=x\cdot y. [/imath] And that translates back to [imath] (ac)\,|\,(bd) [/imath] by the same principle as at the beginning, using the meaning of the notation [imath] s\,|\,t. [/imath]

The general argument is pretty much the same as in many proofs:

1. Check the given conditions. [imath] a\,|\,b [/imath]
2. Rewrite them by their definitions. [imath] a\cdot x=b [/imath]
3. Combine them into a new statement by using the properties that you have. [imath] a(bc)=(ab)c [/imath] and [imath] a x= x a [/imath]
4. Reuse the definition. [imath] (ac)\cdot (xy)=bd [/imath] means [imath] (ac)\,|\,(bd). [/imath]

 

[Dr.Peterson]

What I've covered in proofs says that you ASSUME the hypothesis is true and proceed with that assumption. And by the definition of divisibility:

We say integer [imath]a \neq 0[/imath] divides integer b if and only if there exists an integer m such that [imath]a \times m = b[/imath].

So if we ASSUME the hypothesis is true and use the definition above, why can't you make the substitution for b and d?

Because you substituted in the conclusion, which you don't know to be true, rather than in a hypothesis!

You need to only assume the hypothesis, not the conclusion.

You can rewrite parts of the conclusion, in order to see what you need to prove, but you assumed the conclusion itself to be true:

Then substituting [imath]ax[/imath] for [imath]b[/imath] and [imath]cy[/imath] for [imath]d[/imath], I end up with [imath](\: ac \:) | (\:axcy\:)[/imath]. Rearranging I get [imath](\:ac \:) | (\: acxy)[/imath] and [imath](\:ac \:) | (\: ac(xy))[/imath] where [imath]x \times y[/imath] is an integer because x and y are integers.

Dividing both sides by [imath](\:ac \:)[/imath] gives [imath]1\: | (\: xy)[/imath].

You substituted in (ac) | (bd), which you don't know to be true, and then made an inference from that, which is invalid. All you showed was that if (ac) | (bd), then 1 | (xy).

The other answers deal with what you should do; I'm focusing on your specific question, which was what you did wrong. This is what was most wrong. You should mostly focus on the former, which will teach you correct methods.