Modigliani
New member
- Joined
- Dec 20, 2008
- Messages
- 6
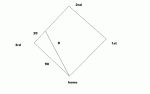
Player running between 2nd base and 3rd at a speed of 20 ft/sec at 20 feet from 3rd. Rate of change in distance from home plate = ?
D^2 = x^2 + y^2
x = distance from 2nd to player
y = length of side (90)
D = sqrt(70^2 + 90^2)
D = 10 * sqrt(130)
2D*dD/dt = 2x*dx/dt + 2y * dy/dt
D*dD/dt = x*dx/dt
(10*sqrt(130))*dD/dt = 70*20
dD/dt = 1200 / (10*sqrt(130))
This isn't right. What went wrong?
D^2 = x^2 + y^2
x = distance from 2nd to player
y = length of side (90)
D = sqrt(70^2 + 90^2)
D = 10 * sqrt(130)
2D*dD/dt = 2x*dx/dt + 2y * dy/dt
D*dD/dt = x*dx/dt
(10*sqrt(130))*dD/dt = 70*20
dD/dt = 1200 / (10*sqrt(130))
This isn't right. What went wrong?