Distance from center of circle to edge of offset 2nd circle by degrees

[jimjohn]

I hope someone can shed some light on this.

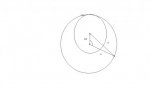
Pic to show what I am doing with the circles...
http://i53.tinypic.com/2vmvfqr.jpg

I need to come up with a formula to calculate the distance from the center of the smaller circle to the edge of the larger circle by degrees. For example we know at 180 degree the answer would be 4-3/4". I need to be able to enter any degree around the circle and return the distance from the center of smaller circle to edge of larger circle.

Anyone have any ideas on how to accomplish this.

Thanks in advance for any help.

 

[galactus]

Try using the law of cosines.

\(\displaystyle d=\sqrt{4^{2}+(3/4)^{2}-2(4)(3/4)cos(\theta)}=\frac{\sqrt{265-96cos(\theta)}}{4}\)

 

[soroban]

Hello, jimjohn!

I need to come up with a formula to calculate the distance from the center of the smaller circle
to the larger circle by degrees. .I need to be able to enter any degree around the circle
and return the distance from the center of smaller circle to edge of larger circle.

If I understand the probem correctly, we don't need the smaller circle.

                  |
                * * *    P
            *     |     o
          *       |   o   *
         *        | o @    *
    - - - - - - - * - - - - - -
        *        O|         *
        *         *(0,-¾)   *
        *         |         *
                  |
         *        |        *
          *       |       *
            *     |     *
                * * *
                  |

We have a circle with center \(\displaystyle \left(0,\,-\frac{3}{4}\right)\) and radius 4.

We want the length of radius vector \(\displaystyle O\!P\) in terms of angle \(\displaystyle \theta.\)


The equation of the circle is: .\(\displaystyle x^2 + (y + \frac{3}{4})^2 \:=\:16\)

Convert to polar coordinates: .\(\displaystyle (r\cos\theta)^2 + (r\sin\theta + \frac{3}{4})^2 \:=\:16\)

. . \(\displaystyle r^2\cos^2\!\theta + r^2\sin^2\!\theta + \frac{3}{2}r\sin\theta + \frac{9}{16} \:=\:16\)

. . \(\displaystyle r^2\underbrace{(\cos^2\!\theta + \sin^2\!\theta)}_{\text{This is 1}} + \frac{3}{2}r\sin\theta - \frac{247}{16} \:=\:0\)

Multiply by 16: .\(\displaystyle 16r^2 + 24\sin\theta\!\cdot\!r - 247 \:=\:0\)

\(\displaystyle \text{Solve for }r\!:\;\;r \;=\;\dfrac{\text{-}24\sin\theta \pm\sqrt{(24\sin\theta)^2 - 4(16)(\text{-}247)}}{2(16)} \;=\;\) \(\displaystyle \dfrac{\text{-}24\sin\theta \pm \sqrt{576\sin^2\theta + 15808}}{32}\)

. . . . . . . . . . \(\displaystyle r \;=\;\dfrac{\text{-}24\sin\theta \pm8\sqrt{9\sin^2\theta + 247}}{32} \;=\;\dfrac{\text{-}3\sin\theta \pm\sqrt{9\sin^2\theta + 247}}{4}\)


From my graph, I assume we want the positive value of \(\displaystyle r.\)

 

[jimjohn]

Galactus, you nailed it first try. I got it working perfectly. Of course after I remembered to convert angle to radian angle. Thanks a ton for both your help in figuring it out.