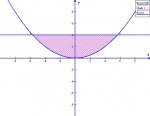
Find the volume of the solid whose base is the region bounded by the parabola x^2=8y and the line y=4, and each plane section perpendicular to the y-axis is an equilateral triangle. (which has an area of sqrt(3)/4 * s^2 i believe)
I've gone through this many times now and I can't seem to set the integral up properly, using both shells and disks...
Please help me
I've gone through this many times now and I can't seem to set the integral up properly, using both shells and disks...
Please help me