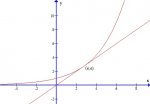
1. For which a > 0 does the curve y = a[sup:329hiy5d]x[/sup:329hiy5d] intersect the line y = x?
2. For which a > 0 is it true that a[sup:329hiy5d]x[/sup:329hiy5d] >= x + 1 for all real numbers x?
3. For what values of k does the equation e[sup:329hiy5d]2x[/sup:329hiy5d] = k * (x)[sup:329hiy5d]1/2[/sup:329hiy5d]
I have worked for hours on each problem. My teacher gave me the hint of using the equation f(x) = a[sup:329hiy5d]x[/sup:329hiy5d] - x for the first one, and using its derivative to solve the problem. I always seem to run into trouble with the fact that both a and x can change..
any help is greatly appreciated. Thanks!
2. For which a > 0 is it true that a[sup:329hiy5d]x[/sup:329hiy5d] >= x + 1 for all real numbers x?
3. For what values of k does the equation e[sup:329hiy5d]2x[/sup:329hiy5d] = k * (x)[sup:329hiy5d]1/2[/sup:329hiy5d]
I have worked for hours on each problem. My teacher gave me the hint of using the equation f(x) = a[sup:329hiy5d]x[/sup:329hiy5d] - x for the first one, and using its derivative to solve the problem. I always seem to run into trouble with the fact that both a and x can change..
any help is greatly appreciated. Thanks!