I.ve been working on this problem for a week but haven't gotten very far. Any help is appreciated
For R>0 a curve in yz plane given by the parametric equation. y(u) = Rsinu and z(u) = R(ln tan u/2 + cosu) for 0<u<

is called a tractrix. The (half) pseudosphere of radius R is the surface obtained by rotating the tractrix about the z axis; the pseudosphere has a patch.
 for 0<u<pi/2 and 0<v<2pi
for 0<u<pi/2 and 0<v<2pi
Let
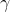 be a curve on the pseudosphere defined by
be a curve on the pseudosphere defined by
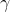 (t) = /sigma (pi/4, t) where 0<t<2pi
(t) = /sigma (pi/4, t) where 0<t<2pi
a.) find the first fundamental form of sigma
b.) find the surface area of the pseudosphere
c.) find the 2nd fundamental form of sigma
d.) find the grodesic curvature k of the curve
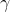
For R>0 a curve in yz plane given by the parametric equation. y(u) = Rsinu and z(u) = R(ln tan u/2 + cosu) for 0<u<
is called a tractrix. The (half) pseudosphere of radius R is the surface obtained by rotating the tractrix about the z axis; the pseudosphere has a patch.
Let
a.) find the first fundamental form of sigma
b.) find the surface area of the pseudosphere
c.) find the 2nd fundamental form of sigma
d.) find the grodesic curvature k of the curve
