derivatives

[jmsic]

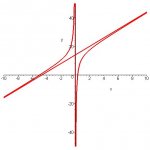
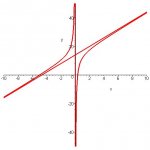
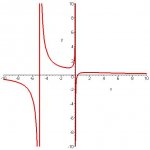
when f(x) = (3 - 1/x)/(x+5) and you are finding y prime would you go ahead and change the 1/x into x[sup:2tvp6zwm]-1[/sup:2tvp6zwm] and find y prime using the quotient rule or would you multiply the top and bottom by x first and then use the quotient rule... cuz i got different answers when i did them differently T_T

please help meeeee

 

[BigGlenntheHeavy]

$\displaystyle f(x) \ = \ (3-\frac{1}{x})(x+5)$

$\displaystyle D_x\bigg[(3-\frac{1}{x})(x+5)\bigg] \ = \ (3-\frac{1}{x})(1)+(x+5)(\frac{1}{x^{2}})$

$\displaystyle = \ 3-\frac{1}{x}+\frac{1}{x}+\frac{5}{x^{2}} \ = \ 3+\frac{5}{x^{2}}$

$\displaystyle f(x) \ = \ (3-\frac{1}{x})(x=5) \ = \ (\frac{3x-1}{x})(x+5) \ = \ \frac{3x^{2}+14x-5}{x}$

$\displaystyle f \ ' \ (x) \ = \ \frac{x(6x+14)-(3x^{2}+14x-5)(1)}{x^{2}} \ = \ \frac{6x^{2}+14x-3x^{2}-14x+5}{x^{2}} \ = \ \frac{3x^{2}+5}{x^{2}} \ = \ 3+\frac{5}{x^{2}}$

$\displaystyle Note: \ No \ critical \ points, \ but \ two \ asymptotes, \ what \ are \ they? \ See \ graph.$

[attachment=1:1imj7unc]abc.jpg[/attachment:1imj7unc]

\(\displaystyle Oops, \ I \ misread \ the \ function.\\)

$\displaystyle f(x) \ = \ \frac{(3-\frac{1}{x})}{(x+5)} \ = \ \frac{3x-1}{x^{2}+5x}$

$\displaystyle f \ ' \ (x) \ = \ \frac{(x^{2}+5x)(3)-(3x-1)(2x+5)}{(x^{2}+5x)^{2}} \ = \ \frac{3x^{2}+15x-6x^{2}-13x+5}{(x^{2}+5x)^{2}}$

$\displaystyle = \ \frac{-3x^{2}+2x+5}{(x^{2}+5x)^{2}} \ = \ -\frac{3x^{2}-2x-5}{x^{2}(x+5)^{2}}$

$\displaystyle Two \ critical \ points, f \ ' \ (-1) \ = \ 0, \ f \ ' \ (5/3) \ = \ 0, \ see \ graph.$

[attachment=0:1imj7unc]zzz.jpg[/attachment:1imj7unc]

 

[jmsic]

i have a question... couldnt you also do it like:
f(x) = 3-x[sup:23pleh4g]-1[/sup:23pleh4g] ALL OVER x + 5
f prime = (x+5) (x[sup:23pleh4g]-2[/sup:23pleh4g]) - (3-x[sup:23pleh4g]-1[/sup:23pleh4g]) ALL OVER (x+5)[sup:23pleh4g]2[/sup:23pleh4g]
f prime = 2x[sup:23pleh4g]-1[/sup:23pleh4g] + 5x[sup:23pleh4g]-2[/sup:23pleh4g] + 3 ALL OVER (x+5)[sup:23pleh4g]2[/sup:23pleh4g]

 

[BigGlenntheHeavy]

\you can solve it any way that pleases you as long as you get the right answer.