You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Derivatives
- Thread starter Karni
- Start date
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,393
My answer is that it is differentiable for all x = 0. Double check me on this but here's what I have.Are the partial derivatives defined? If so, what are their values?
Take the partial of f(x, y) by x. You will have to expand the sines and cosines in terms of their power series but you should find that the derivative does not exist for x = 0.
-Dan
Thank you Dan !
Forgot to add that the derivatives are asked regarding the point (0, pie) .
You are saying they do exist for any value of y so long as x=0?
My answer is that it is differentiable for all x = 0. Double check me on this but here's what I have.
Forgot to add that the derivatives are asked regarding the point (0, pie) .
You are saying they do exist for any value of y so long as x=0?
My answer is that it is differentiable for all x = 0. Double check me on this but here's what I have.
Take the partial of f(x, y) by x. You will have to expand the sines and cosines in terms of their power series but you should find that the derivative does not exist for x = 0.
-Dan
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,393
I haven't specifically checked for [imath](0, \pi )[/imath], but that x partial at 0 isn't likely to exist for any y. I don't have time to double check that right now. Perhaps later.Thank you Dan !
Forgot to add that the derivatives are asked regarding the point (0, pie) .
You are saying they do exist for any value of y so long as x=0?
My answer is that it is differentiable for all x = 0. Double check me on this but here's what I have.
(By the way [imath]\pi[/imath] is spelled "pi.")
-Dan
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
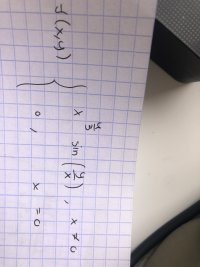
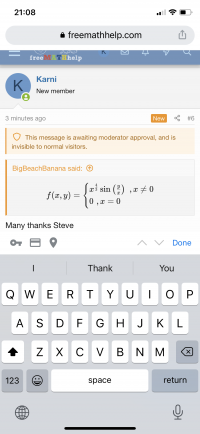
[math]f(x,y)=\begin{cases} x^{\frac{4}{3}}\sin\left(\frac{y}{x}\right)\,\,,x\neq 0\\ 0\,\,,x=0 \end{cases}[/math]It would be a lot easier to help you if the problem was posted right side up.
Many thanks Steve[math]f(x,y)=\begin{cases} x^{\frac{4}{3}}\sin\left(\frac{y}{x}\right)\,\,,x\neq 0\\ 0\,\,,x=0 \end{cases}[/math]
It would be a lot easier to help you if the problem was posted right side up.