Derivative with Absolute Value

[turophile]

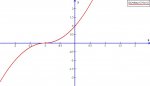
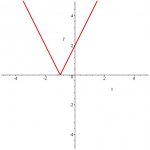
I'm trying to find the root of the first derivative of f(x) = (x + 1)|x + 1|. Here's what I've done so far:

f' = |x + 1| ? [d/dx (x + 1)] + (x + 1) ? (d/dx |x + 1|)
= |x + 1| ? 1 + (x + 1) ? (d/dx sqrt[(x + 1)[sup:ns3igxed]2[/sup:ns3igxed]])
= |x + 1| + (x + 1) ? 1/2 ? 1/sqrt[(x + 1)[sup:ns3igxed]2[/sup:ns3igxed]] ? d/dx (x + 1)[sup:ns3igxed]2[/sup:ns3igxed]
= |x + 1| + (x + 1) ? 1/2 ? 1/sqrt[(x + 1)[sup:ns3igxed]2[/sup:ns3igxed]] ? 2(x + 1) ? d/dx (x + 1)
= |x + 1| + (x + 1) ? 1/2 ? 1/sqrt[(x + 1)[sup:ns3igxed]2[/sup:ns3igxed]] ? 2(x + 1) ? 1
= |x + 1| + (x + 1)[sup:ns3igxed]2[/sup:ns3igxed]/|x + 1| ? 0
? |x + 1| = – (x + 1)[sup:ns3igxed]2[/sup:ns3igxed]/|x + 1|
? |x + 1|[sup:ns3igxed]2[/sup:ns3igxed] = – (x + 1)[sup:ns3igxed]2[/sup:ns3igxed]

Now I'm in a situation where the square of x + 1 equals the negative of the square of x + 1. Since I'm working with real numbers, I think this is OK as long as x + 1 = 0, that is, x = - 1. Did I get the correct answer?

 

[galactus]

Yes, you did T.

Here's the graph. You can easily see the 0 slope at x=-1

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ (x+1)|x+1| \ = \ (x+1)[(x+1)^2]^{1/2}.\)

\(\displaystyle Hence, \ f'(x) \ = \ (1)[(x+1)^2]^{1/2} \ + \ (x+1)(1/2)[(x+1)^2]^{-1/2}(x+1)(2)\)

\(\displaystyle f'(x) \ = \ |x+1|+\frac{(x+1)^2}{|x+1|} \ = \ \frac{2|x+1|^2}{|x+1|} \ = \ 2|x+1|\)

\(\displaystyle When \ f'(x) \ = \ 0, \ x \ = \ -1, \ see \ graph.\)

[attachment=0:2puwq7is]fff.jpg[/attachment:2puwq7is]