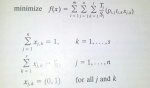Hello,
I´m not sure where my question belongs, so I´m sorry if this is the wrong category.
I am trying to apply the "dedicated storage assignment problem" to a real situation in my company to relocate articles in our storage to optimize storage/retrieval distances. I found this problem formulation in the literature:
s = number of storage slots of locations
n = number of products to be stored
m = number of input/output (I/O) points
Sj = storage requirement for product j, expressed in the number of storage slots
Tj = throughput requirement or activity level for product j, expressed by the number of storage/retrievals performed per unit time
pi,j = percent of the storage/retrieval trips for product j that are from/to input/output (I/O) point i
ti,k = time required to travel between I/O point i and storage/retrieval location k
xj,k = 1, if product j is assigned to storage/retrieval location k
= 0, otherwise
f(x) = expected time required to satisfy the throughput requirements for the system
I attached the formulation of the problem as a picture.
(source: Francis et al., 1992)
The book says the procedure is based on the assumption that "all products being stored have the same percentage distribution of movement between the storage/retrieval locations and the I/O points."
In my case I would like to assume that some I/O points are supply destinations. Each destination has a different distance to the storage area and a different article demand. My question: Is it possible to reformulate the formula so that the articles can be assigned to certain I/O points?
Thank you!
13
I´m not sure where my question belongs, so I´m sorry if this is the wrong category.
I am trying to apply the "dedicated storage assignment problem" to a real situation in my company to relocate articles in our storage to optimize storage/retrieval distances. I found this problem formulation in the literature:
s = number of storage slots of locations
n = number of products to be stored
m = number of input/output (I/O) points
Sj = storage requirement for product j, expressed in the number of storage slots
Tj = throughput requirement or activity level for product j, expressed by the number of storage/retrievals performed per unit time
pi,j = percent of the storage/retrieval trips for product j that are from/to input/output (I/O) point i
ti,k = time required to travel between I/O point i and storage/retrieval location k
xj,k = 1, if product j is assigned to storage/retrieval location k
= 0, otherwise
f(x) = expected time required to satisfy the throughput requirements for the system
I attached the formulation of the problem as a picture.
(source: Francis et al., 1992)
The book says the procedure is based on the assumption that "all products being stored have the same percentage distribution of movement between the storage/retrieval locations and the I/O points."
In my case I would like to assume that some I/O points are supply destinations. Each destination has a different distance to the storage area and a different article demand. My question: Is it possible to reformulate the formula so that the articles can be assigned to certain I/O points?
Thank you!
13