Decide derivative in a point

[AnyHelpIsAppreciated]

I hope this is the right section for this question!

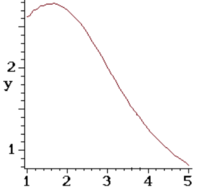
Question: The point (3,2) is on the curve in the x,y plane with the equation ((y^3)/x + x^2*y=62/3). Near this point is a graph to the function y(x). Decide y'(3).An illustration of the curve near the point (3,2) can be seen in the attached photo.

I started by derivating the function and solving y'(x) (with wolframalpha) and got y'(x)=((y^3-2*x^3*y)/(x^3+3*x*y^2)) where y=y(x). I then put in x=3 and y(3)=2 since its the point (3,2) and got that y'(3)=-106/99. But that is the wrong answer.
Could anyone help me out and tell me how they calculated and what answer they got?
Thanks in advance!

 

[LCKurtz]

Whenever I see an expression written like this: ((y^3)/x + x^2*y=62/3) on these help boards, my first thought is that the problem is likely not transcribed correctly. You don't usually see parentheses around both sides of an equation. Please post an image of the original problem. Also include your steps toward the solution.

 

[mmm4444bot]

Hello AnyHelpIsAppreciated. Are you member Nivelo?

\(\;\)

 

[Otis]

… (y^3)/x + x^2*y = 62/3 …

… where y = y(x) …

… I started by derivating the function …

Hello AHIA. Function y(x) has not been provided directly (it is implicit, in the given equation). What function did you use for y(x), when finding its first derivative?

… [wolframalpha gave me] y'(x) = (y^3 - 2*x^3*y)/(x^3 + 3*x*y^2). I then put in x=3 and [y=2] … and got …

y'(3) = -106/99

When x=3 and y=2, the expression (y^3-2*x^3*y)/(x^3+3*x*y^2) does not equal -106/99.

Also, that expression is not y'(x).

At this point, I can't help you because you haven't shown what you entered at the wolframalpha site. By the way, does the assignment instruct you to use technology to answer the exercise?

?

 

[AnyHelpIsAppreciated]

Hello AHIA. Function y(x) has not been provided directly (it is implicit, in the given equation). What function did you use for y(x), when finding its first derivative?



When x=3 and y=2, the expression (y^3-2*x^3*y)/(x^3+3*x*y^2) does not equal -106/99.

Also, that expression is not y'(x).

At this point, I can't help you because you haven't shown what you entered at the wolframalpha site. By the way, does the assignment instruct you to use technology to answer the exercise?

?

I mad a mistake , the function is ((y^3)/x -2*x^3*y)=62/3

 

[LCKurtz]

Why do you expect to receive help when you ignore our responses? I posted the first response and asked you to:
1. Provide an image of the problem. Or you could type it exactly.
2. Show the steps you took to get your answer.

You have done neither.

 

[Otis]

I [made] a mistake , the function is (y^3)/x - 2*x^3*y = 62/3

Hello. That is not a function statement; it is an equation containing two variables.

You did not answer any of my questions. Please complete the forum's request to read the guidelines, and then follow them.

Assuming that you're allowed to use technology for evaluating y'(3), ask wolframalpha to solve the given equation for y. The result will be y(x).

Next, ask wolframalpha to differentiate y(x). The result will be y'(x), and you can then evaluate y'(3).

?

 

[HallsofIvy]

I mad a mistake , the function is ((y^3)/x -2*x^3*y)=62/3

This is getting more and more confusing! In your first post you say "The point (3,2) is on the curve in the x,y plane with the equation ((y^3)/x + x^2*y=62/3)." in the next sentence you say "Near this point is a graph to the function y(x)" (emphasis added).

Now you tell us the function should be "((y^3)/x -2*x^3*y)=62/3". (3, 2) is not on either graph because 2^3/3+ 3^2(2)= 8/3+ 54= 170/3, not 62/3 and 2^3/3- 2(2^3)3= 27/3- 48= (27+ 144)/3= 171/3, also far from 62/3..

 

[Otis]

… in the next sentence you say "Near this point is a graph to the function y(x)" …

Yes, the presentation is confusing. After AHIA changed the equation, I'd considered commenting that (3, 2) is not really near (3, 6.1) on the revised function's graph, but then I wondered what 'near' really means here. I'd like to see an image of the original material.

Also, the exact value of y'(3) does not look like something a student would be expected to find by hand.