cylinder n sphere

[red and white kop!]

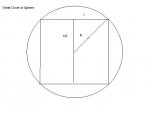
a circular cylinder is to fit inside a sphere of radius 10cm. calculate the maximum possible volume of the cylinder. (it is probably best to take as your indpendent variable the height or half the height of the cylinder).
i'm stuck here cos i don't know where to start. i drew a section of the both to try and find a clue but i'm lost. any hints?

 

[BigGlenntheHeavy]

\(\displaystyle red \ and \ white \ kop! \ A \ trick. \ I \ found \ when \ working \ this \ type \ of \ problem \ to \ employ\)

\(\displaystyle the \ great \ circle \ of \ a \ sphere, \ thereby \ reducing \ the \ problem \ from \ 3 \ dimensional \ to \ 2\)

\(\displaystyle dimensional. \ See \ graph \ below \ of \ great \ circle.\)

[attachment=0:1hatex0y]xxx.JPG[/attachment:1hatex0y]

\(\displaystyle Hence \ R^2 \ = \ r^2 \ + \ (h/2)^2 \ \implies \ r^2 \ = \ R^2 \ - \ h^2/4\)

\(\displaystyle V_{cyl} \ = \ \pi r^2 h \ = \ \pi[h(R^2-h^2/4)] \ = \ \pi[hR^2-h^3/4]\)

\(\displaystyle Now, \ when \ R \ = \ 10cm., \ we \ have \ V \ = \ \pi[100h-h^3/4]\)

\(\displaystyle Ergo, \ \frac{dV}{dh} \ = \ \pi[100-3h^2/4] \ = \ 0 \ \implies \ h \ = \ \frac{20\sqrt3}{3}\)

\(\displaystyle Now, \ I \ assume \ that \ you \ can \ take \ it \ from \ here.\)

 

[red and white kop!]

thats what i meant by a section
anyway thanks this really helps