Curve Sketching

[thumbs137]

So my math teacher gave us a quick little review on this today, but I can't even figure out the first question of my assignment.
I guess that my first question is, "what is the difference, or is there any, between extreme values, critical points, endpoints, and points of interest?"
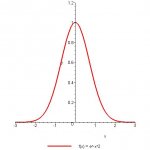
The first question on my assignment is use the analytic method to fine extreme functions and where they occur for the function k(x)= e^-x^2. Do I need to take the derivative? My teacher said something about finding the domain, but I don't understand what that has to do with anything...

your help would definitely be appreciated!
~thumbs

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ e^{-x^{2}}, \ f \ ' \ (x) \ = \ -2xe^{x^{2}}\)

\(\displaystyle Setting \ the \ slope \ = \ to \ 0, \ we \ get: \ -2xe^{x^{2}} \ = \ 0, \ x \ = \ 0, \ hence \ f(0) \ = \ 1 \ = \ max.\)

\(\displaystyle y \ = \ 0 \ is \ a \ horizontal \ asymptote \ and \ domain \ is \ (-\infty,\infty), \ range \ is \ (0,1].\)

\(\displaystyle Note: \ See \ graph \ below.\)

[attachment=0:47h65gdl]def.jpg[/attachment:47h65gdl]

 

[thumbs137]

OK. Thanks. But why did I need to find the domain and range? Is it supposed to help me understand something? And what defines a extreme point? Is it just any point that is used to sketch the graph?

 

[BigGlenntheHeavy]

\(\displaystyle Hey \ pal \ I \ don't \ read \ peoples' \ minds \ (your's \ or \ your \ Professor), \ I \ just \ showed \ you \ some \ of \ the\)

\(\displaystyle \ properties \ of \ f(x).\)

 

[thumbs137]

I know. thank you. I guess i'm just trying to understand why it works and what it means. thanks for you help though.