Cubic polynomials.

[Rumor]

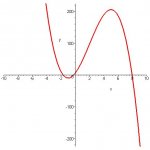
Eh. Here's the problem:

"A cubic polynomial is given by f(x)=ax^3+bx^2+30x+k where a, b, and k are constants. The function f(x) has a local minimum at (-1,-10) and a point of inflection at x=2.

a) Find the values of a, b, and k.

b) Use the second derivative to verify that (-1,-10) really is a local minimum for your function.

c) Find the location of any local maximums for your function. Verify that they are indeed a local maximum."

Here's what I've done so far..

I've found the first derivative, f(x)= 3ax^2 + 2bx + 30
and the second derivative, f(x)= 6ax + 2b.

I then plugged the value of x=1 into the first derivative, getting 3a-2b+30.
I also plugged the inflection point of x=2 into the second derivative and got
12a+2b.

From there, I can't seem to remember what to do. Help, please? D:

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ ax^{3}+bx^{2}+30x+k\)

\(\displaystyle f \ ' \ (x) \ = \ 3ax^{2}+2bx+30\)

\(\displaystyle f \ " \ (x) \ = \ 6ax+2b\)

\(\displaystyle Now, \ f(-1) \ = \ -10 \ = \ -a+b-30+k \ \implies \ -a+b+k \ = \ 20\)

\(\displaystyle f \ ' \ (-1) \ = \ 0 \ = \ 3a-2b+30 \ \implies \ 3a-2b \ = \ -30\)

\(\displaystyle f \ " \ (2) \ = \ 0 \ = \ 12a+2b\)

\(\displaystyle Hence, \ using \ substitution \ or \ elimination \ we \ arrive \ at \ a=-2, \ b=12, \ and \ k=6.\)

\(\displaystyle Ergo, \ f(x) \ = \ -2x^{3}+12x^{2}+30x+6, \ see \ graph \ below.\)

[attachment=0:28kqzpwl]ugly.jpg[/attachment:28kqzpwl]

 

[JeffWest]

Once you have found your a,b,k values use the completed function f(x)=-2x^3+12x^2+30x+6 to verify your inflection point is actually at 2.

Inflection points are found from the second derivative test, that is to set the second derivative equal to zero and solve for x.

\(\displaystyle f'(x)=-6x^2+24x+30\)

and

\(\displaystyle f''(x)=-12x^2+24\)


You can then use the first derivative to verify the given minimum and then find the other local max by setting it equal to zero and solving for y.

(correction was made to the formating of this Post)
My apologies I was just starting out and didn't know how to type functions. I do now though. Thanks for the help BigGlenntheHeavy

 

[BigGlenntheHeavy]

\(\displaystyle f'(x) \ = \ -6x^{2}+24x+30\)

\(\displaystyle f"(x) \ = \ -12x^{2}+24 \ ??????\)