Cube root function pls help me....

[minhthai2312]

y= expression^(1/3) (x)

because i don't know how to include the math equation in here.... so at the equation above mean y= cube root x
=> y= expression^(1/3) (x) = y= cube root (x)
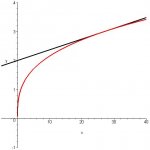
a/ Find an equation of the tangent to the curve y= expression^(1/3) (x) at the point where x=27. Calculate the coordinates of the point where the tangent cuts the x-asix. Verify that it is a tangent by graphing both the cube root function and your equation in graphmatica
b/ let x(0) be any positive number and let Q be the point on the curve y= expression^(1/3) (x) where x=x(0). Find an expression for the point where the tangent at Q intersects with the x-axis / Conclude and make an illustration

Pls help me with that problem....

 

[Deleted member 4993]

y= expression^(1/3) (x)
a/ Find an equation of the tangent to the curve y= expression^(1/3) (x) at the point where x=27. Calculate the coordinates of the point where the tangent cuts the x-asix. Verify that it is a tangent by graphing both the cube root function and your equation in graphmatica
b/ let x(0) be any positive number and let Q be the point on the curve y= expression^(1/3) (x) where x=x(0). Find an expression for the point where the tangent at Q intersects with the x-axis / Conclude and make an illustration

You need to post the exact problem as it was presented to you.

Then

Please share your work with us, indicating exactly where you are stuck so that we know where to begin to help you.

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ x^{1/3}, \ f \ ' \ (x) \ = \ \frac{1}{3x^{2/3}}.\)

\(\displaystyle f \ ' \ (27) \ = \ \frac{1}{27} \ = \ m, \ f(27) \ = \ 3.\)

\(\displaystyle (27,3), \ m \ = \ \frac{1}{27}.\)

\(\displaystyle y-3 \ = \ \frac{1}{27}(x-27),\ y \ = \ \frac{x}{27}+2.\)

\(\displaystyle See \ graph.\)

[attachment=0:z5ewcjso]none.jpg[/attachment:z5ewcjso]