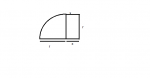red and white kop!
Junior Member
- Joined
- Jun 15, 2009
- Messages
- 231
the cross section of an object has the shape of a quarter-circle of radius r adjoining a rectangle of width x and height r, as shown in the diagram.
a. the perimeter and area of the cross-section are P and A respectively. express each of P and A in terms of r and x and hence show that A=0.5Pr -r^2
this part was easy, P= 2r+2x+0.5(pi)(r), A= rx + 0.25(pi)(r)^2
b. taking the perimeter P as fixed, find x in terms of r for the case when the area A of the cross section is a maximum, and show that, for this value of x, A is a maximum and not a minimum.
here i don't know where to start, i dont understand how to combine the equations i have. it seems almost impossible to get one differentiable equation with two given equations and 4 variables! can someone work me through this?
a. the perimeter and area of the cross-section are P and A respectively. express each of P and A in terms of r and x and hence show that A=0.5Pr -r^2
this part was easy, P= 2r+2x+0.5(pi)(r), A= rx + 0.25(pi)(r)^2
b. taking the perimeter P as fixed, find x in terms of r for the case when the area A of the cross section is a maximum, and show that, for this value of x, A is a maximum and not a minimum.
here i don't know where to start, i dont understand how to combine the equations i have. it seems almost impossible to get one differentiable equation with two given equations and 4 variables! can someone work me through this?