Critical points of function

[bambambvp1234]

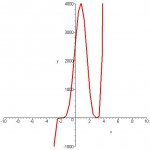
How many critical points does the function f(x)= (x+2)[sup:39cy84gr]5[/sup:39cy84gr](x-3)[sup:39cy84gr]4[/sup:39cy84gr] have
A. One
B. two
C. three
D.five
E. nine

I derived the function using the product rule and got

5(x+2)[sup:39cy84gr]4[/sup:39cy84gr](x-3)[sup:39cy84gr]4[/sup:39cy84gr] + (x+2)[sup:39cy84gr]5[/sup:39cy84gr] 4(x+2)[sup:39cy84gr]3[/sup:39cy84gr]

then factored

(x+2)[sup:39cy84gr]4[/sup:39cy84gr](x-3)[sup:39cy84gr]3[/sup:39cy84gr]((5(x-3)+4(x+2)))

Im not sure how many solutions that makes for critical points

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ (x+2)^{5}(x-3)^{4}\)

\(\displaystyle f \ ' \ (x) \ = \ 5(x+2)^{4}(x-3)^{4}+4(x+2)^{5}(x-3)^{3}\)

\(\displaystyle = \ (x+2)^{4}(x-3)^{3}(9x-7) \ = \ 0\)

\(\displaystyle Hence, \ three \ critical \ points: \ f \ ' \ (-2) \ = \ 0, \ f \ ' \ (3) \ = \ 0, \ and \ f \ ' \ (7/9) \ = \ 0.\)

See graph:

[attachment=0:3ivi2gnd]uuu.jpg[/attachment:3ivi2gnd]

 

[bambambvp1234]

Thanks for ur response i see i didnt combine like terms, ur response really helped a lot