Creating new formula for the area of an isosceles triangle

[Vara1803]

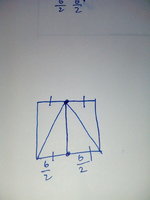
(View the picture)in that isosceles triangle I drew another 3 lines so that the upper line has the exact same length as the base of the triangle and other two for connecting that upper line to the base of the triangle which will give us an rectangle. By the property of the isosceles triangle the point of the triangle will divide the upper line into two equal parts which is nothing but b÷2 (if you want you can draw another picture like this and check) and the other two lines are nothing but height of the triangle. Now we can find the height of the triangle by using Pythagorean theorem (as the rectangle will give us another two right angled triangle as given in the pic)and h is = to the square root of( a^2)-(b^2)÷4 and substituting h as this in the formula of 1÷2 ×b×h. Now we can find the area of an isosceles triangle without finding height of that triangle

 

[skeeter]

but you did find the height of the triangle ...

[math]h = \sqrt{a^2 - \dfrac{b^2}{4}}[/math] is also the perpendicular distance from the vertex angle to the base.

 

[JeffM]

I am not quite sure what you are trying to say.

Yes, the vertical sides of the rectangle = the height of the isosceles triangle.

You then multiply 1/2, the height, and the base to find the area. That is certainly not finding a new formula for area.

I suspect what you are discussing is that there is a different way to find the height than by bisecting the angle opposite the base. Nice.

EDIT: I suspect you should prove that the apex of the triangle bisects the the top horizontal of the rectangle. It is essential to your proof. You should then prove that the height of the triangle is equal to the verticals of the rectangle. As I said, it is a nice piece of insight, but maybe the proof needs to be a bit tighter.

 

[Vara1803]

but you did find the height of the triangle ...

[math]h = \sqrt{a^2 - \dfrac{b^2}{4}}[/math] is also the perpendicular distance from the vertex angle to the base.

I

I am not quite sure what you are trying to say.

Yes, the vertical sides of the rectangle = the height of the isosceles triangle.

You then multiply 1/2, the height, and the base to find the area. That is certainly not finding a new formula for area.

I suspect what you are discussing is that there is a different way to find the height than by bisecting the angle opposite the base. Nice.

EDIT: I suspect you should prove that the apex of the triangle bisects the the top horizontal of the rectangle. It is essential to your proof. You should then prove that the height of the triangle is equal to the verticals of the rectangle. As I said, it is a nice piece of insight, but maybe the proof needs to be a bit tighter.

(You then multiply 1/2, the height, and the base to find the area. That is certainly not finding a new formula for area.) I substituted the value of h(square root of a^2-b^2÷4)in that formula which makes it renewed which gives us area without needing the value of h(like without measuring height of the triangle with physical means we can just find it by this formula which saves us loads of time and energy) and about the proofs (1) I said that I have drawn the upper line with exact length of the base and The altitude to the base of an isosceles triangle bisects the base(view that 1 st
pic)the points will divide them into two equal parts.(2)see the second pic(any vertical line parallel to the breadth touching both lengths inside a rectangle is equal to breadth) see the third pic And thank you for your response

 

[Vara1803]

but you did find the height of the triangle ...

[math]h = \sqrt{a^2 - \dfrac{b^2}{4}}[/math] is also the perpendicular distance from the vertex angle to the base.

I substituted the value of h(square root of a^2-b^2÷4)in the formula 1÷2 ×b×h which makes it renewed which gives us area without needing the value of h(like without measuring height of the triangle with physical means we can just find it by this formula which saves us loads of time and energy)

 

[JeffM]

The area formula you use is (1/2)hb. That is a general formula that applies to any triangle. Your proof depends on that formula. You have not created a new formula for computing the area of an isosceles triangle. You even say "substituting h" in your first post.

And if the triangle is isosceles, all you ever have to do to find the length of h is to measure a and b. You do not have to measure h independently. All of your talk about saving time and energy is complete nonsense. There is no need whatsoever to construct your rectangle; that is extra work and effort.

[MATH]h = \sqrt{a^2 - 0.25b^2}.[/MATH]
If you bisect the angle opposite the base and drop the bisecting line to the base, you necessarily split the isosceles triangle into two congruent right triangles each with a leg of b/2 and a hypotenuse of a. The other leg is h. The Pythagorean Theorem thus lets you compute the length of h, no measurement required.

At first, I thought it was neat that you had developed a different way to find h even though it is less efficient. Now I see that you really did not have a clue on what you were doing.