Creating functions from word problems

[Spazzerella]

HI all, new user here. I am totally stumped on 2 hw problems and desperate for help. Since it's late Sunday night here (Hawaii), there is no one on the campus tutoring service.

For both problems the master instructions are:
A) write a "let x = .... " statement
B) write an appropriate function (this is where I am totally hung up)
C) complete the square for the formula and identify its vertex. (I'm good with this step)
D) answer the problem in complete sentence. (I can obviously manage this once I understand the dang problems)
The problems are as follows:

1) The perimeter of a rectangle is 20 feet. Find the dimensions for which the diagonal is as short as possible. Also, find the length of this shortest diagonal. Solve by using the Pythagorean theorem.

What I have thus far (it's not much, I know):

Let x = width and y = length therefore, 2x + 2y = 20 feet. If I solve for y I get, y=10-x. So, I think the function should be something like this: 2x + 2(10-x), but that doesn't seem to work out. I also know that the PT is a^2 + b^2 = c^2, but I have no idea how to incorporate that into this problem.

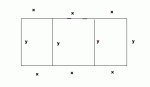
2) Suppose that you have 1000 feet of fencing with which to build three adjacent pig pens as shown (the picture shows one large rectangle with two internal divisions). Find the dimensions so that the total area is as large as possible.

What I have thus far (once again, not much):

Let x = width and y = length, therefore 1000 feet = 4x + 2y. If I solve for y I get y = 500 - x. I'm stumped from there.




Thanks so much.

 

[galactus]

The rectangle will be optimized when the rectangle is a square.

But, you seem to have the idea.

The diagonal has length \(\displaystyle \sqrt{x^{2}+y^{2}}=z\).............[1]

We want to optimize z.

The perimieter is \(\displaystyle 2x+2y=20\Rightarrow x+y=10\)

\(\displaystyle y=10-x\)

Sub into [1] so that it is in terms of one variable, x:

\(\displaystyle x^{2}+(10-x)^{2}=z\)

\(\displaystyle \frac{dz}{dx}=2x-10\)

\(\displaystyle 2x-10=0\Rightarrow x=5\)

This means the other three sides have length 5 as well. So, it is a square.

The diagonal has length:

\(\displaystyle \sqrt{5^{2}+5^{2}}=5\sqrt{2}\)

You do not have to use calculus though. The equation from [2] is a parabola. Use \(\displaystyle x=\frac{-b}{2a}\) to find the vertex and, thus, the optimum value.


Try the same sort of idea with the other problem. Set up the equation you're optimizing, then use the perimeter information to eliminate a variable.

 

[Spazzerella]

I ended up using the function for area for both problems to find the max/min values. I don't have my work in front of my any longer, so I am not sure what the first function was, but for the second I used:

a(x) = x( -2x -500) and then completed the square.

 

[galactus]

Let the length of each section be x. Let the width be y.

Thus, the area is A=3xy

The perimeter is \(\displaystyle 4y+6x=1000\Rightarrow y=250-\frac{3x}{2}\)

\(\displaystyle A=3x(250-\frac{3x}{2})=-\frac{9x^{2}}{2}+750x\)

By using the formula for the x coordinate of the vertex of a parabola, \(\displaystyle x=\frac{-b}{2a}, \;\ y=c-\frac{b^{2}}{4a}\)

\(\displaystyle x=\frac{-750}{2(\frac{-9}{2})}=\frac{250}{3}=83.\overline{3}\)

Thus, \(\displaystyle y=250-\frac{3(\frac{250}{3})}{2}=125\)

Here is a graph. I labeled each section so you can see why the PERIMETER is 6x+4y.