Hi! Im new to this forum so forgive me if i chose the wrong section. Also i dont have any real degree in mathematics other than my gymnasial exams in Sweden.
I have been working on a google sheet for abit and ive ended up with a Correlation matrix (i think the name is?) that i need to be clustered in a certain way.
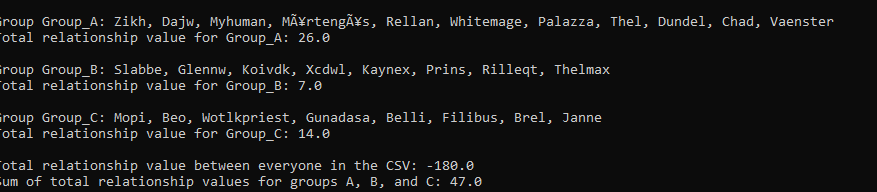
The sheet is containing members and their relation towards eachothers, ive posted a picture to see.
Currently there is 34 different members in the sheet, and i need to divide it into 3 groups with the goal of obtaining the least possible "relationship" value..
That means that the total of each group combined needs to be the lowest value possible. To add to this it doesent matter how big the groups are, if the groups combined get a lower value by stacking 20 members in 1 group, 10 in the other and 4 in the last, that is totaly fine.
Ive spend countless of hours working on this, and so far ive only learnt the name of my table (correlation matrix), and that i need some way of clustering it.
Ive read some into K-Means clustering and i think that its a reasonal way of dealing with my task.? There is also something called agglomeration clustering which i havent gotten as deep into.
Anyway, i post here to see if someone knows about a software or a way for me to solve my problem. Let me know, thanks
William.P
I have been working on a google sheet for abit and ive ended up with a Correlation matrix (i think the name is?) that i need to be clustered in a certain way.
The sheet is containing members and their relation towards eachothers, ive posted a picture to see.
Currently there is 34 different members in the sheet, and i need to divide it into 3 groups with the goal of obtaining the least possible "relationship" value..
That means that the total of each group combined needs to be the lowest value possible. To add to this it doesent matter how big the groups are, if the groups combined get a lower value by stacking 20 members in 1 group, 10 in the other and 4 in the last, that is totaly fine.
Ive spend countless of hours working on this, and so far ive only learnt the name of my table (correlation matrix), and that i need some way of clustering it.
Ive read some into K-Means clustering and i think that its a reasonal way of dealing with my task.? There is also something called agglomeration clustering which i havent gotten as deep into.
Anyway, i post here to see if someone knows about a software or a way for me to solve my problem. Let me know, thanks
William.P