You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
coorrdinates of centroid of region bounded by y-axis, y=x,
- Thread starter alex83
- Start date
- Joined
- Feb 4, 2004
- Messages
- 16,550
Duplicate post.
What formula(s) or algorithm(s) have they given you for this process? How far have you gotten in computing the moments?
Please be complete. Thank you!
What formula(s) or algorithm(s) have they given you for this process? How far have you gotten in computing the moments?
Please be complete. Thank you!
Start by finding the area of the said region.
\(\displaystyle \text{Area=}\int_{0}^{1}\int_{x}^{\frac{2}{x^{2}+1}}dydx\)
Then, \(\displaystyle \overline{x}=\frac{1}{\text{Area}}\int\int x \;\ dA\)
\(\displaystyle \overline{y}=\frac{1}{\text{Area}}\int\int y \;\ dA\)
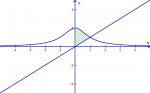
The graph shows the region you must find the centroid of.
\(\displaystyle \text{Area=}\int_{0}^{1}\int_{x}^{\frac{2}{x^{2}+1}}dydx\)
Then, \(\displaystyle \overline{x}=\frac{1}{\text{Area}}\int\int x \;\ dA\)
\(\displaystyle \overline{y}=\frac{1}{\text{Area}}\int\int y \;\ dA\)
The graph shows the region you must find the centroid of.
Attachments
thanks but if i have the area and want to avoid the double integrals how do i solve ??
\
the formula and method that our professor use is (MOMENTS )
where first he finds -lenght (which i cant fiqure out here )
- width which is dx here (i believe so )
-area which i already got and = (PI-1)/2
- mass or dm which is = delta * area
then Mx = integral y^~ dm
My = integral x^~ dm
M = integral dm
last
x= my/m
y=mx/m
this is the method we use in class but i couldnt plug it in this problem
thnx
\
the formula and method that our professor use is (MOMENTS )
where first he finds -lenght (which i cant fiqure out here )
- width which is dx here (i believe so )
-area which i already got and = (PI-1)/2
- mass or dm which is = delta * area
then Mx = integral y^~ dm
My = integral x^~ dm
M = integral dm
last
x= my/m
y=mx/m
this is the method we use in class but i couldnt plug it in this problem
thnx
thanks for ur reply
but i was trying this before i checked ur answer would u check it pls
first i set both equations equal to each other and got : x^3+x-2=0 ; solve it and got x=1
the question is i found these formulas in the book and want to set them up
Mx= 1/2 integral [a-b] g^2(x) - f^2(x) dx
My = integral [a-b] x(g(x)-f(x)) dx
M=integral [a-b] g(x)-f(x)
then set X=My/M and Y=Mx/M
is it right to use these in this problem ??
what should the integral limits[a-b] be ?? should it be [0-1]??/
but i was trying this before i checked ur answer would u check it pls
first i set both equations equal to each other and got : x^3+x-2=0 ; solve it and got x=1
the question is i found these formulas in the book and want to set them up
Mx= 1/2 integral [a-b] g^2(x) - f^2(x) dx
My = integral [a-b] x(g(x)-f(x)) dx
M=integral [a-b] g(x)-f(x)
then set X=My/M and Y=Mx/M
is it right to use these in this problem ??
what should the integral limits[a-b] be ?? should it be [0-1]??/