Hello, I tried a lot to solve this problem but I have not solved it yet. I want somebody help me solving this problem and tell me the right answer please:
Consider the solid S described below.
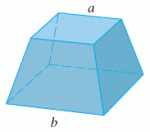
A frustum of a pyramid with square base of side b = 7, square top of side a = 5, and height h = 5.
a)Find the volume V of this solid.
V =
b)What happens if a = b? (Enter your answer in terms of b and h.)
we get a ( sphere, tetrahedron, cap of sphere, rectangular solid , square pyramid )
with volume V =
C) What happens if a = 0? (Enter your answer in terms of b and h.)
we get a ( sphere, tetrahedron, cap of sphere, rectangular solid , square pyramid )
with volume V =
Consider the solid S described below.
A frustum of a pyramid with square base of side b = 7, square top of side a = 5, and height h = 5.
a)Find the volume V of this solid.
V =
b)What happens if a = b? (Enter your answer in terms of b and h.)
we get a ( sphere, tetrahedron, cap of sphere, rectangular solid , square pyramid )
with volume V =
C) What happens if a = 0? (Enter your answer in terms of b and h.)
we get a ( sphere, tetrahedron, cap of sphere, rectangular solid , square pyramid )
with volume V =