Conics

[Aladdin]

As I pointed before, that I'll take summer lessons for the preperation of next year subjects . I started a new topic(lesson) called Conics.As we know every beginning has a start .

The question ::

Determine the equation of the conic C(F,d,e).Determine the nature of C(F,d,e) and its different elements.
Given:
F(3,1)
Equation of directrix : x-1= >0
Eccentricity :\(\displaystyle \frac{\sqrt2}{2}\)

My work is the following :

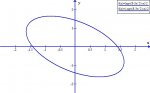
I ploted the given focus(3,1) and graphed the directrix x=1,knowing the e = c/a = sqrt(2)/2 --> c =sqrt2 & a =2 .But since 0<e<1 - so this is an Ellips(correct?)

The length of the major axis is 2a = 2(2)=4 ...

The equation is :
\(\displaystyle \frac{(x-1)^2}{4}+\frac{(y-1)^2}{2} = 1\)

IS MY WORK CORRECT ? MISSING SOMETHING? - Thanks in advance-

Aladdin,

 

[galactus]

Unless I am missing something, that looks good.

Here is a tidbit to keep in mind since you're working with conics. The eccentricity of a parabola is 1, all the time.

That may be a clue if you're ever given a similar problem such as this and they tell you the eccentricity = 1.

For a parabola as well, the focus is at \(\displaystyle F\left(h, \;\ k+\frac{1}{4a}\right)\), where h and k are the vertex coordinates.

Just some food for thought in case it's needed somewhere along the line.

 

[Aladdin]

For a parabola as well, the focus is at \(\displaystyle F\left(h, \;\ k+\frac{1}{4a}\right)\), where h and k are the vertex coordinates.

Where is K ??

 

[galactus]

It's there. I had an errant slash which made it not display.

 

[Aladdin]

It's there. I had an errant slash which made it not display.

Oh okay -- So my work is correct ?? . Just a question is conics a basic subject to be learned ?

 

[galactus]

Yes, I suppose, when it comes to geometry. Often, it is touched upon when one starts CalcIII, or somewhere near that.

It involves ellipses, hyperbolas, parabolas, and so forth. It also involves what shape you get when they are sliced by a plane. For instance, when we pass a plane through a cone, we get a parabola or an ellipse depending on the angle of the plane. I remember once I had this challenging related rates problem, I used the fact that if we slice a cone with a plane, we get a parabola. You know the famous related rates problem when they ask how fast the water is rising when a cone is being filled with water and so forth. Well, that's easy if the cone is apex down. What about if it's laying on its side?. That was the tricky part.
So, in certain areas it can prove useful to know conics. I like them.

 

[Aladdin]

Yes, I suppose, when it comes to geometry. Often, it is touched upon when one starts CalcIII, or somewhere near that.

It involves ellipses, hyperbolas, parabolas, and so forth. It also involves what shape you get when they are sliced by a plane. For instance, when we pass a plane through a cone, we get a parabola or an ellipse depending on the angle of the plane. I remember once I had this challenging related rates problem, I used the fact that if we slice a cone with a plane, we get a parabola. You know the famous related rates problem when they ask how fast the water is rising when a cone is being filled with water and so forth. Well, that's easy if the cone is apex down. What about if it's laying on its side?. That was the tricky part.
So, in certain areas it can prove useful to know conics. I like them.

Thanks Cody, Conics is my first lesson that I took by my self ( on the internet) and I'll start with my new math teacher this monday .I like them also.

 

[galactus]

Did you know we can use a discriminant to find out what kind of conic we have when we are given an equation.

Say we have \(\displaystyle x^{2}+xy+y^{2}-2=0\)

By taking the discriminant we can see what it is.

\(\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\)

If \(\displaystyle B^{2}-4AC<0\), then it's an ellipse, circle, a point, or else has no graph.

If \(\displaystyle B^{2}-4AC>0\), then it is a hyperbola, or a pair of intersecting lines.

If \(\displaystyle B^{2}-4AC=0\), then it is a parabola, a line, a pair of lines, or has no graph.

Take the example. \(\displaystyle B=1, \;\ A=1, \;\ C=1\)

\(\displaystyle (1)^{2}-4(1)(1)=-3\)

It is less than 0, so it is an ellipse, point, or no graph.

It has a graph. \(\displaystyle y=\frac{\sqrt{8-3x^{2}}-x}{2}, \;\ y=\frac{\sqrt{8-3x^{2}}-x}{2}\)

Here's the graph. It's a tilted ellipse.

There is a small conics lesson for the day

 

[Aladdin]

Did you know we can use a discriminant to find out what kind of conic we have when we are given an equation.

Say we have \(\displaystyle x^{2}+xy+y^{2}-2=0\)

By taking the discriminant we can see what it is.

\(\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\)

If \(\displaystyle B^{2}-4AC<0\), then it's an ellipse, circle, a point, or else has no graph.

If \(\displaystyle B^{2}-4AC>0\), then it is a hyperbola, or a pair of intersecting lines.

If \(\displaystyle B^{2}-4AC=0\), then it is a parabola, a line, a pair of lines, or has no graph.

Take the example. \(\displaystyle B=1, \;\ A=1, \;\ C=1\)

\(\displaystyle (1)^{2}-4(1)(1)=-3\)

It is less than 0, so it is an ellipse, point, or no graph.

It has a graph. \(\displaystyle y=\frac{\sqrt{8-3x^{2}}-x}{2}, \;\ y=\frac{\sqrt{8-3x^{2}}-x}{2}\)I think you meant \(\displaystyle y=\frac{-\sqrt{8-3x^{2}}-x}{2}\) But how did you get that:?

Here's the graph. It's a tilted ellipse.

There is a small conics lesson for the day

 

[Aladdin]

The same question with different given:

Given:F(-3,-1)

Equation of the directrix : x+1=0

Eccentricity : e = 1

My work :

Since the eccentricity equals 1 so it's a parabola.Now :

I graphed the directrix x=-1 & plotted the focus .

Now the equation is in the conicial system (S, i(vector) , j(vector) ) --> the equation in this case is

\(\displaystyle y^2=4ax=2px \ p \ is \ the \ parameter \ of \ the \ conic\), So which one I use -- what is the value of a ?

Thanks in advance,
Aladdin