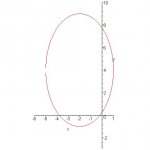
Im told to find the center, vertices, foci, and eccentricity of the conic section given by this equation: 25x^2 + 9y^2 + 100x -72y + 19 = 0
i split the y's and x's then i complete the square for each.. so at the end i get
[9(y-4)^2]+[25(x+2)^2]=1
i believe this is an ellipse.. but im lost on how to graph it because i thought the standard formula of an ellipse would be in form of [(x^2)/(a^2)] + [(y^2)/(b^2)] = 1
i split the y's and x's then i complete the square for each.. so at the end i get
[9(y-4)^2]+[25(x+2)^2]=1
i believe this is an ellipse.. but im lost on how to graph it because i thought the standard formula of an ellipse would be in form of [(x^2)/(a^2)] + [(y^2)/(b^2)] = 1