Conceptual Trouble

[clannkelly]

EDIT: I'm sorry, for some reason my pictures don't seem to be working. I'll try to look into it later when I've got more time.<br>
<br>
I just started Calculus I at university. It's been two weeks already and I'm still having an extremely difficult time with the concepts my teacher keeps presenting to me. I've never been a bad math student, but I do tend to run into trouble if I don't understand the purpose/point of the problems I'm working on. I was hoping someone on this forum could re-explain some basic calculus concepts to me. I'll list them below.<br>
<br>
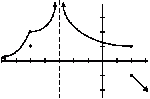
1.<br><img src="http://www.freemathhelp.com/forum/attachment.php?attachmentid=1660&stc=1" attachmentid="1660" alt="" id="vbattach_1660" class="previewthumb"><br>
This graph will help illustrate what I'm talking about. I understood the concept that as x approaches 2, the limit of f(x) is 2. Then, my teacher said that as x approaches 1, the limit of f(x) is 1. That didn't make sense to me, as there isn't a hole at f(x) = 1. I asked my teacher about it, and he said that that was because the function value and the limit value are the same at x=1 for f(x). I don't understand how that can happen. If there is a functional value for a given value of x, how can it also be a limit? I understood that a limit was a value that f(x) approaches as x approaches a certain number, but that f(x) never actually touches that limit. If the graph is touching the limit, how can it BE a limit? Isn't it just another part of the function?<br>
<br>
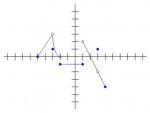
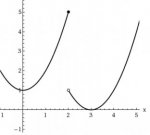
2. My teacher isn't a very wordy person, so he tends to avoid word problems in his assignments. He'll give us graphs like these:<br><img src="http://www.freemathhelp.com/forum/attachment.php?attachmentid=1661&stc=1" attachmentid="1661" alt="" id="vbattach_1661" class="previewthumb"><img src="http://www.freemathhelp.com/forum/attachment.php?attachmentid=1662&stc=1" attachmentid="1662" alt="" id="vbattach_1662" class="previewthumb"><img src="http://www.freemathhelp.com/forum/attachment.php?attachmentid=1663&stc=1" attachmentid="1663" alt="" id="vbattach_1663" class="previewthumb"><img src="http://www.freemathhelp.com/forum/attachment.php?attachmentid=1664&stc=1" attachmentid="1664" alt="" id="vbattach_1664" class="previewthumb"><br>
<br>
And ask us to find the limit, or something of that nature. I can usually do that, but I don't understand what it is I'm doing. Would it be possible for someone to describe to me what graphs like these would represent? Or, what kinds of real-world problems are solved and/or represented through the use of calculus/limits? I've looked this up before, but I've never gotten a clear answer. The most I can understand is that physicists use equations and graphs like this, but for what? If you have to use big words, don't worry about it. I would rather have big words than none at all. Another common graph he gives us is a series of horizontal lines, staggered like stairs. That usually represents the amount of some substance in a person's bloodstream over a given amount of time, and that makes sense to me. When I only have the visuals but not an explanation of what they represent, I get very easily confused by what it is I'm supposed to be figuring out. I'm not expecting a full description of these graphs in particular; they're only examples. I was really hoping for someone to describe a time when calculus, limits or derivatives came in handy for them, or were used on the job. Any help you can give me is greatly appreciated.<br>
<br>
3. This isn't so much a concept, but I was hoping for some clarification on this topic. It's about factoring out or otherwise playing with a function in order to evaluate the limit as something other than 0/0. This seems to happen a lot; for example, the question "lim as x-->1 of x^2-1 / x-1". If x equals 1, then the limit is 0/0, which is apparently not a correct answer. So, you play around with it and you end up with lim as x-->1 of x+1, which comes out to 2. Just so I'm clear, are x^2-1 / x-1 and x+1 the same function? If so, would the graph of the first one have no limit and the graph of the second have a limit? They seem identical.<br>
<br>
I'm sure I'll have a lot more questions as time goes by, but for now, I think that'll do. <img src="images/smilies/icon_wink.gif" border="0" alt="" title="" smilieid="4" class="inlineimg">

 

[clannkelly]

I'm sorry, I tried to fix my pictures and for some reason my entire post disappeared. I'm not much of an internet guru. I think I've got it now, though. The graph for number one was this:



And the graphs for number two looked like this:


In response to your first response, Jeff, yes, it's a bad habit of mine to overthink the glaringly obvious. I suppose the idea of a limit does make sense, I just don't understand exactly why it's an important idea, or what applications it has. Functions make sense to me, because they seem to help solve problems. For example, say you knew that you needed one can of paint to cover 2 square metres of wall (hypothetically, of course). So, you would use the function f(x) = 2x to figure out how many cans of paint you needed. That seems like a pretty practical application. What kind of practical application would a limit have? A limit is definitely a nifty idea, but I don't understand exactly what kind of problem they're supposed to solve. They seem to create more trouble than they cure

Your explanation brought up another question. The quote was:
"The function

exists at x = 4, but the function's limit is 0 at x = 4 because it f(x) = 0 for all values of x close to but not equal to 4, which means that f(x) is certainly close to 0."

Are f(x) = 0 and f(x) =1 the same function? It doesn't seem like they could be, but I've only ever encountered functions that have one solution, like x=0 OR x=1, but not both. It doesn't really fit in with my idea of a function that it would have two solutions, so there must be some disconnect there.

Thank you for your help, Jeff. You did clear up a few questions I had, but every answer brings up a new question.

 

[clannkelly]

So \(\displaystyle f(x) = 0\ if x \neq 4, and\ f(x) = 1\ if\ x = 4\) is a perfectly good function. It is completely unambiguous; it gives a unique value for any specified value of x. Just like the function above, however, it does not give the same answer for every value of x. The reason that this function looks strange to you is that it is not continuous.

Ahh, that makes sense. My teacher didn't make that distinction at all. He's explained continuous and discontinuous functions, but only in graph form. It helps to have it explained in equation form.

I didn't think you were criticizing me at all, don't worry It really is true; I've done that my whole life. I've always had trouble understanding things that are too simple. I also have trouble with showing my work, because it all seems so obvious to me.