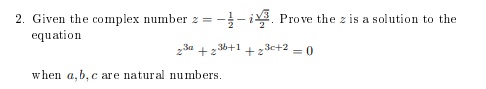Complex numbers are just another extension of the concept of number, just as real numbers are an extension of the concept of number. The main things to remember with complex numbers is that there is no order property and that
[MATH]i^2 = -\ 1 = (-\ i)^2.[/MATH]
So to start things off. I would notice that [MATH]z^{3a} = (z^3)^a.[/MATH]
I would then calculate:
[MATH]z^3 = \left ( - \dfrac{1}{2} - \dfrac{i\sqrt{3}}{2} \right )^3 = \dfrac{1}{8} * (-\ 1 - i\sqrt{3})^3 = [/MATH]
[MATH]\dfrac{1}{8} * (-\ 1 - i\sqrt{3})(-\ 1 - i\sqrt{3})^2 = \dfrac{1}{8} * (-\ 1 - i\sqrt{3})(1 + 2i\sqrt{3} + 3i^2 ) =[/MATH]
[MATH]\dfrac{1}{8} * (-\ 1 - i\sqrt{3})(1 - 3 + 2i\sqrt{3}) = \dfrac{1}{8} * (-\ 1 - i\sqrt{3})(-\ 2 + 2i\sqrt{3}) =[/MATH]
[MATH]\dfrac{2}{8} * (-\ 1 - i\sqrt{3})(-\ 1 + i\sqrt{3}) = \dfrac{1}{4} * \{(-\ 1)^2 - (i * \sqrt{3})^2\}) =[/MATH]
[MATH]\dfrac{1}{4} * \{1 - 3(i^2)\} = \dfrac{1}{4} * \{1 - 3(-\ 1)\} = \dfrac{1}{4} * 4 = 1. [/MATH]
Now you may have memorized that
[MATH]\sqrt[3]{1 \pm 0 * i} = -\ \dfrac{1}{2} - \dfrac{i\sqrt{3}}{2} = \sqrt[3]{1 \pm 0 * i} = \sqrt[3]{1}.[/MATH]
But why bother memorizing anything, when you calculate it.
And [MATH]z^{3a} = (z^3)^a = 1^a = 1.[/MATH]
Now notice that
[MATH]z^{(3b+1)} = z * z^{3b} = z * (z^3)^b = z * 1^b = z = -\ \dfrac{1}{2} - \dfrac{i\sqrt{3}}{2}.[/MATH]
And [MATH]z^{(3c+2)} = z^2 * z^{3c} = z^2 * 1 = z^2 = \left ( -\ \dfrac{1}{2} - \dfrac{i\sqrt{3}}{2} \right )^2 =[/MATH]
[MATH]\dfrac{1}{4} + 2 * \dfrac{(-\ 1) * (-\ i \sqrt{3})}{2 * 2} + \dfrac{3i^2}{4} = \dfrac{1}{4} - \dfrac{3}{4} + \dfrac{2i\sqrt{3}}{4} = -\ \dfrac{1}{2} + \dfrac{i\sqrt{3}}{2}.[/MATH]
Now what happens when you add all that up?
Complex numbers involve a lot of mechanics, but the mechanics are an old story.