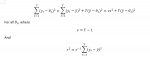gabrielwong1991
New member
- Joined
- Jan 18, 2015
- Messages
- 9
Basically I have this equation and trying to prove it from the middle bit to the LHS.
This derivation is actually when I do bayesian econometrics where we need to find the conjugate normal analysis with unknown mean and known variance for the prior.
I was told we can use completing the square to prove it but after many attempt I fail to recognise...
Perhaps anyone could help?
I also tried the completing the square like this notes but with no success.
http://www.cse.psu.edu/~rtc12/CSE598C/completingTheSquare.pdf
Many thanks
. . . . .\(\displaystyle \large \displaystyle \sum_{t = 1}^T\, (y_t\, -\, \theta_1)^2\, =\, \sum_{t = 1}^T\, (y_t\, -\, \bar{y})^2\, +\, T\, (\bar{y}\, -\, \theta_1)^2\, =\, vs^2\, +\, T\, (\bar{y}\, -\, \theta_1)^2\)
\(\displaystyle \large \mbox{For all }\, \theta_1,\, \mbox{ where}\)
. . . . .\(\displaystyle \large v\, =\, T\, -\, 1\)
\(\displaystyle \large \mbox{And}\)
. . . . .\(\displaystyle \large s^2\, =\, v^{-1}\, \)\(\displaystyle \displaystyle \sum_{t = 1}^T\, (y_t\, -\, \bar{y})^2\)
This derivation is actually when I do bayesian econometrics where we need to find the conjugate normal analysis with unknown mean and known variance for the prior.
I was told we can use completing the square to prove it but after many attempt I fail to recognise...
Perhaps anyone could help?
I also tried the completing the square like this notes but with no success.
http://www.cse.psu.edu/~rtc12/CSE598C/completingTheSquare.pdf
Many thanks
. . . . .\(\displaystyle \large \displaystyle \sum_{t = 1}^T\, (y_t\, -\, \theta_1)^2\, =\, \sum_{t = 1}^T\, (y_t\, -\, \bar{y})^2\, +\, T\, (\bar{y}\, -\, \theta_1)^2\, =\, vs^2\, +\, T\, (\bar{y}\, -\, \theta_1)^2\)
\(\displaystyle \large \mbox{For all }\, \theta_1,\, \mbox{ where}\)
. . . . .\(\displaystyle \large v\, =\, T\, -\, 1\)
\(\displaystyle \large \mbox{And}\)
. . . . .\(\displaystyle \large s^2\, =\, v^{-1}\, \)\(\displaystyle \displaystyle \sum_{t = 1}^T\, (y_t\, -\, \bar{y})^2\)
Attachments
Last edited: