Probability
Full Member
- Joined
- Jan 26, 2012
- Messages
- 432
I have two equations, the first one is y = 7x + 44/2, and the second one is y = - 1x - 22/2
I want to find the value of "x" by combining these two equations, if the word "combining" is chosen correctly?
So I have tried it two ways, they are;
7x + 44/2 = -1x - 22/2
7x + 44 = -1x - 44/2
7x + 88 = -1x - 44
7x = - 1x - 132
x = - 16.5
That was my first way of doing it, then I tried the opposite way by changing the equations round.
-1x - 22/2 = 7x + 44/2
-1x - 22 = 7x + 88/2
-1x - 44 = 7x + 88
-1x = 7x + 132
x = -16.5
I seem to get the same answer each way although I think I am solving for "x" correctly.
If I put in my "x" compoent value into either of the equations I should find the "y" value.
-1(-16.5) - 11 = -16.5 - 11 = -27.5
So the coordinates for my centre of a circle look like (-16.5, -27.5)
The radius would be;
r^2 = (-16.5 - 0)^2 + (-27.5 - 0)^2 = 1028.5
Sqrt = 32
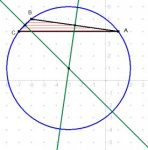
Given originally that my coordinates were A(1, 4) B(-6, 5) and C(-7, 4), where I was asked to find the midpoints of the lines AB and BC, thus the perpendicular bisectors of AB and BC, then find the centre of the circle, I feel that I am not getting something quite right when I get a radius of 32 based on the coordinates above?
I would appreciate any second opinions thanks
I want to find the value of "x" by combining these two equations, if the word "combining" is chosen correctly?
So I have tried it two ways, they are;
7x + 44/2 = -1x - 22/2
7x + 44 = -1x - 44/2
7x + 88 = -1x - 44
7x = - 1x - 132
x = - 16.5
That was my first way of doing it, then I tried the opposite way by changing the equations round.
-1x - 22/2 = 7x + 44/2
-1x - 22 = 7x + 88/2
-1x - 44 = 7x + 88
-1x = 7x + 132
x = -16.5
I seem to get the same answer each way although I think I am solving for "x" correctly.
If I put in my "x" compoent value into either of the equations I should find the "y" value.
-1(-16.5) - 11 = -16.5 - 11 = -27.5
So the coordinates for my centre of a circle look like (-16.5, -27.5)
The radius would be;
r^2 = (-16.5 - 0)^2 + (-27.5 - 0)^2 = 1028.5
Sqrt = 32
Given originally that my coordinates were A(1, 4) B(-6, 5) and C(-7, 4), where I was asked to find the midpoints of the lines AB and BC, thus the perpendicular bisectors of AB and BC, then find the centre of the circle, I feel that I am not getting something quite right when I get a radius of 32 based on the coordinates above?
I would appreciate any second opinions thanks