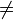Hi guys, I'd need to know how to perform these exercises. Tomorrow I have the exam but I did not understand how to do these two:
If your class has arrived at the exam, then you should have at least
some idea of how at least to
start these exercises. :shock:
a.) How many x € Z with 100100 <= x <= 999 000 are such that x contains 12 as in expression and
There is exactly one digit repeated at least twice.
I will guess that the text of this exercise, had it been written originally in English, would have been something like this:
1. Let x be a whole number, with 100,000 < x < 999,000. Suppose that two of the digits of x are "12", in this order and immediately next to each other. Suppose also that at least one digit of x is repeated at least twice. How many such numbers x are there?
If this is a valid interpretation of your translation, then a good place to start might be to work with cases. What numeral, from 0 to 9, can
not be the first (that is, the largest) digit? If the "12" does not begin the number (such as "120,000"), how many options do you have for the first digit? And so forth.
What are your thoughts? What have you tried? How far have you gotten? Where are you stuck?
b.) How many solutions are there of the equation x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 = 2021, where
x1,. . . , X8 and x1 € Z,. . . , X8> = 0, with 50 <= x2 <= 100, 30 <= x3 <= 40, x4> = 10, 30 <= x6 <= 70,
x1 + x3 + x5 = 789 and x3 + x6 = / (different) 110?
I'm not sure what is meant here. Perhaps some of the translation was typed out of order...? My guess is as follows:
2. Consider the equation:
. . . . .x1 + x2 + x3 + x4 + x5 + x7 + x8 = 2,021
...where each variable represents a non-negative integer, with the following restrictions:
. . . . .50 < x2 < 100
. . . . .30 < x3 < 40
. . . . .10 < x4
. . . . .30 < x6 < 70
. . . . .x1 + x3 + x5 = 789
. . . . .x3 + x6 \(\displaystyle \, \neq\,\) 110
Under these conditions, how many solutions exist for the original equation?
Is this correct?
When you reply, please include a clear statement of your efforts so far, so we can see where you're getting stuck. Thank you! :wink: