Win_odd Dhamnekar
Junior Member
- Joined
- Aug 14, 2018
- Messages
- 212
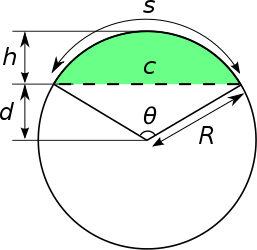
Using the above figure, I want to prove the following formulaes.
1) The chord length is
2)The saggita is
3)The angle is
Lastly, The area A of the circular segment \(A=R^2*\left(\arcsin{\frac{c}{2R}}-\frac{c}{2R}*\sqrt{1-(\frac{c}{2R})^2}\right)=R\left(\arccos\frac{d}{R}-d\sqrt{1-\frac{d^2}{R^2}}\right)\)
