Checking answer: Volume of Solid using disk/washer method

S

SeekerOfDragons

New member
Joined
Oct 8, 2009
Messages
46
I'm trying to verify another answer to a different problem than the one listed here elsewhere on the board.

the problem reads:

Use the disk/washer method to set up the integral that represents the volume of the solid formed by revolving the region bounded by:

2x + 2y = 5
y = 1/x

revolve around y = 1/2 (do not evaluate the integral)

Solved for Y on the first equation and came up with: y = (5 - 2x)/2

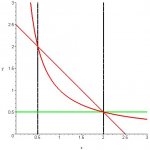
I then set the two functions equal to each other to determine where they intersected and came up with (1/2, 2) and (2, 1/2). using that information, I graphed the problem and determined that the washer method was needed to solve the problem.

the integral I came up with for this problem is:

pi * integral [1/2, 2] [( (1/x - 1)^2 ) - ( (5-2x)/2 - 1)^2 ] dx

hoping I'm correct? but not 100% sure.

r/

SoD
 
\(\displaystyle \pi\int_{1/2}^{2}\bigg[\bigg(\frac{5-2x}{2}-\frac{1}{2}\bigg)^{2}-\bigg(\frac{1}{x}-\frac{1}{2}\bigg)^{2}\bigg]dx\)

\(\displaystyle See \ Graph.\)

[attachment=0:36bxzw7v]ghi.jpg[/attachment:36bxzw7v]
 

Attachments

  • ghi.jpg
    ghi.jpg
    24 KB · Views: 438
Gah! and that's what happens when you're in a hurry to finish a problem. y=(5-2x)/2 is the outermost function from where it's being rotated and it's being revolved around 1/2 not 1. grrr.
 
ok, once again I'm confused after looking at the picture again... We're rotating the shape around y = 1/2. Which means it's being spun vertically about y = 1/2. If that's the case, isn't y = 1/x always the outer most function? if it was being spun around x=2 then I would imagine that y = (5-2x)/2 would be the outermost function...

still slightly confused...

r/

SoD
 
It's being spun horizontally about y = 1/2.

y=1/2 is the green line.

If we were rotating it around x=2, then it would be spun vertically and you would be right.
 
How is it being spun horizontally around the green line? doesn't horizontal mean left and right? the way I read/understood the problem, it was being spun vertically/up and down around the green line. In that instance, isn't y = 1/x always the furthest function/line away from the point of rotation? and in that case, wouldn't 1/x be the Big Radius and y = (5 - 2x)/2 be the Little Radius?

Maybe i'm not understanding how it's being spun? as it's being depicted in the graph you provided, wouldn't the area be above the green line 1/2 the time, and below the green line the other 1/2? Moving in a top to bottom direction.

If it was being spun around x=2 in a left to right direction the way i understand how it works, then y = (5 - 2x)/2 would be Big Radius...
 
So did i till this morning when I went to rewrite the problem. Looking at the picture I just can't envision how you can spin the shape horizontally around the green line. unless you mean to spin it both horizontally and vertically such that it is being spun down and to the right... but in that instance 1/x would be the furthest half the time and (5 - 2x)/2 would be furthest 1/2 the time?
 
ok, never mind. I'm an idiot.

I totally mis labeled my curves and thought the straight line was 1/x. my thoughts were right, but I had the curves mis labeled and was totally throwing off my solution.

apologies all around for this headache I've caused both you and me.
 
Look at you index finger and put it in an horizontal position (horizon). that is the way it (the problem, y =1/2) is rotated. Now put your index finger in a vertical (up yours) position. That is the way (if x =2) the problem would be rotated.
 
yup. I got it. green line is horizontal, but the shape is moving around it in an up and down manner fixed at (2, 1/2). and if I'd labeled my graph correctly when I drew it, I'd have gotten it right and we'd not have had the headache we did. I just mislabeled my picture and had the wrong function on the outside in my solution...
 
You must log in or register to reply here.
Top