Hello, tlc!
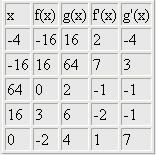
\(\displaystyle \;\;\;x\;\;\,f(x)\;\,g(x)\;\,f'(x)\;\,g'(x)\)
\(\displaystyle \;-16\;\;\;16\;\;\;64\;\;\;7\;\;\;\;\,3\)
\(\displaystyle \;\,-4\;\,-16\;\;\;16\;\;\;\:2\;\;\;-4\)
\(\displaystyle \;\;\;0\;\;-2\;\;\;\;4\;\;\;\;1\;\;\;\;7\)
\(\displaystyle \;\;16\;\;\;\:3\;\;\;\;6\;\;\;-2\;\;\;-1\)
\(\displaystyle \;\;64\;\;\;0\;\;\;\;\,2\;\;\;-2\;\;\;-2\)
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
1. Given: \(\displaystyle \;y\;=\;f(x\cdot f(x))\). . . Find \(\displaystyle y'\) when \(\displaystyle x\,=\,\)-\(\displaystyle 4\)
Use the Chain Rule and the Product Rule, then substitute the values.
\(\displaystyle y'\;=\;f'[x\cdot f(x)]\cdot\left[x\cdot f'(x)\,+\,f(x)\right]\)
\(\displaystyle y'\;=\;f'[\)-\(\displaystyle 4\cdot f(\)-\(\displaystyle 4)] \cdot [\)-\(\displaystyle 4\cdot f'(\)-\(\displaystyle 4)\,+\,f(\)-\(\displaystyle 4) ]\)
\(\displaystyle y'\;=\;f'[ (\)-\(\displaystyle 4)(\)-\(\displaystyle 16)] \cdot [\)-\(\displaystyle 4(2)\,+\,(\)-\(\displaystyle 16)]\)
\(\displaystyle y'\;=\;f'(64)\cdot[\)-\(\displaystyle 8\,-\,16]\)
\(\displaystyle y'\;=\;(\)-\(\displaystyle 1)\cdot[\)-\(\displaystyle 24]\)
\(\displaystyle y'\;=\;24\)
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
2. Given: \(\displaystyle \;y \;= \;\frac{f(x)}{g(x)\,+\,6}\) . . Find \(\displaystyle y'\) when \(\displaystyle x\,=\,\)-\(\displaystyle 16\)
Use the Quotient Rule, then substitute the values.
\(\displaystyle \L y'\;=\;\frac{\left[g(x)\,+\,6\right]\cdot f'(x)\,-\,f(x)\cdot g'(x)}{\left[g(x)\,+\,6\right]^2}\)
\(\displaystyle \L y'\;=\;\frac{[g(-16)\,+\,6]\cdot f'(-16)\,-\,f(-16)\cdot g'(-16)}{[g(-16)\,+\,6]^2}\)
\(\displaystyle \L y'\;=\;\frac{[64\,+\,6]\cdot(7)\,-\,(16)(3)}{(64\,+\,6)^2}\)
\(\displaystyle \L y'\;=\;\frac{(70)(7)\,-\,(16)(3)}{(70^2)}\)
\(\displaystyle \L y'\;=\;\frac{490\,-\,48}{4900}\;=\;\frac{442}{4900}\;=\;\frac{221}{2450}\)