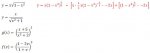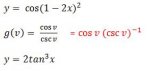Chain Rule Help

[dalasTR]

Find the derivative of the function
I am having a few issues with these problems. If I can get help with how to do the first one or two from each set I'd like to try the rest. My work is below.[attachment=1:2ie5dwjy]pic1.jpg[/attachment:2ie5dwjy][attachment=0:2ie5dwjy]pic2.jpg[/attachment:2ie5dwjy]

Any help is GREATLY appreciated and needed.

 

[BigGlenntheHeavy]

I'll do one for you to get you started.

\(\displaystyle f(v) \ = \ \bigg(\frac{1-2v}{1+v}\bigg)^{3}\)

\(\displaystyle f \ ' \ (v) \ = \ 3\bigg(\frac{1-2v}{1+v}\bigg)^{2}\bigg(\frac{(1+v)(-2)-(1-2v)(1)}{(1+v)^{2}}\bigg)\)

\(\displaystyle = \ 3\frac{(1-2v)^{2}}{(1+v)^{2}}\bigg(\frac{-3}{(1+v)^{2}}\bigg)\)

\(\displaystyle = \ \frac{-9(1-2v)^{2}}{(1+v)^{4}}\)

 

[dalasTR]

Thanks! I was able to solve the third one in the first set with your help. However, I am still stuck on the first two... I do the product rule correct?

 

[dalasTR]

Nevermind I figured them out! Thank you.

Any help on the second set ofquestions?

 

[galactus]

The second one in the last set can be rewritten:

\(\displaystyle \frac{cos(v)}{csc(v)}=sin(v)cos(v)\)

Now, just use the product rule.

 

[BigGlenntheHeavy]

\(\displaystyle g(v) \ = \ \frac{cos(v)}{csc(v)} \ = \ \frac{\frac{cos(v)}{1}}{\frac{1}{sin(v)}} \ = \ cos(v)sin(v)\)

\(\displaystyle Now, g \ ' \ (v ) \ = \ [cos(v)cos(v)]+[sin(v)(-sin(v)] \ = \ cos^{2}(v)-sin^{2}(v).\)