Cavalieri's principle

[dear2009]

hey everybody,


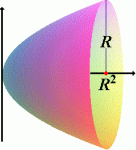
Use Cavalieri’s principle to derive the formula for the volume of a paraboloid with radius R and height R2.

Integrate this from x=0 to x=R2 to find the paraboloid’s volume.

This is what I know I am supposed to do:
Orient the paraboloid so that its axis is the x-axis, and its vertex is at the origin. Then the perpendicular cross sectional area at x (on the x-axis) should be A(x) = px.

The problem is I am stuck after this part.

 

[daon]

I wikipedia'd this and don't see the direct application of that principle.

However, for a paraboloid of circular cross-section centered on the x-axis you have y^2+z^2=a^2x, where a is the radius of the cross section at x=1.

We can use this standard form to create one fitting this model: y^2+z^2=x. So when x=R^2, we get the circle y^2+z^2=R^2, which is what we have pictured.

At a given x, our flat disk has area Pi*r(x)^2, which implies the volume of a thin disk will be: Pi*(z^2+y^2)dx = Pi*x*dx

Then you perform the integral \(\displaystyle \pi \int _0^{R^2}x dx\)