can you help

[mathhelp1a]

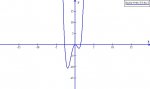
f(x) = x^4 + 4/3 x^ 3 - 4x^2
find and identify the relative extrema of f by applying the second derivative test.

i got relative max at (-2, -10.6) and (1,-1.6)

i got relative min at (0,0)
am i right

 

[galactus]

I think you have the correct points, but have them labeled in reverse.

\(\displaystyle f(x)=x^{4}+\frac{4}{3}x^{3}-4x^{2}\)

By the second derivative test \(\displaystyle f''(0)=-8 \;\ \text{relative maximum}\)

\(\displaystyle f''(1)=12 \;\ \text{relative minimum}\)

\(\displaystyle f''(-2)=24 \;\ \text{relative minimum}\)

See by the graph.

If \(\displaystyle f''(x_{0})>0, \;\ \text{relative minimum}\)

If \(\displaystyle f''(x_{0})<0, \;\ \text{relative maximum}\)

 

[mathhelp1a]

my book says plug those numbers in the original equation, not the second derivative

 

[chrisr]

That's another way to do it, but you'd need to be certain of the shape of the graph.
Say you had a cubic, with a maximum and a minimum.
The maximum will be above the minimum, yes?
So, if you substitute the values of x you get from solving the first derivative = 0,
locating the max and min on the x axis, but not knowing which is which,
you can now find f(x[sub:1jdnikpu]1[/sub:1jdnikpu]) and f(x[sub:1jdnikpu]2[/sub:1jdnikpu]) and whichever is the greater is the max.
Or, if the "overall" graph was going upwards, you'd know the max occurs before the min.

You'd need more analysis with your equation though.
However, since the coefficient of x[sup:1jdnikpu]4[/sup:1jdnikpu] is positive, it dives down to the first minimum,
then up to a max, down to the next min and takes off to infinity again.

Some graphs may have horizontal points of inflexion, though.