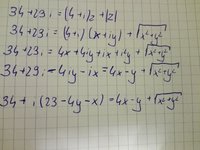Can you help me solve this

[ulqira]

34+29i=(4+i)z+|z|

 

[tkhunny]

Do you know another name for [math]|z|[/math] ?

Have you considered [math]z = a+bi[/math] ?

 

[ulqira]

|z| it is the distance from the center of the coordinate system
I know i should compare real parts and imaginary parts, but i have a problem with that.
34+29i-4iy-ix=4x-y+root(x^2+y^2)
Sorry for my english.

 

[Steven G]

Yes, we will certainly help you solve this. But 1st you need to tell us exactly what you need with, that is where are you stuck?

 

[tkhunny]

Well, you do seem to have the piece I was hoping for. If [math]z = x+yi,\;then\;|z|=\sqrt{x^{2} + y^{2}}[/math]. This is a Real Number.

What is stopping you from collecting Real and Imaginary parts?

 

[ulqira]

I don't know what i should do with root

 

[tkhunny]

I don't know what i should do with root

Why not? It's a Real Number. Treat it like one.

 

[ulqira]

Is this correct?

 

[pka]

34+29i=(4+i)z+|z|

I find that this is a ridiculously tedious exercise. But if one must do it here is a suggestion.
Change to rectangular form: \(\displaystyle 34+29i=(4+i)(x+yi)+|x+yi|\)
Because the real part \(\displaystyle \Re(x,y)=34\) and the imaginary part \(\displaystyle \Im(x,y)=29\)
If \(\displaystyle \Re(x,y)=(4x-y)+\sqrt{x^2+y^2}\) then can you find \(\displaystyle \Im(x,y)~?\)

 

[ulqira]

I don't know if i did it right. If it is good i just have to find y x and i will do it. But i'm sure it is right

 

[pka]

I don't know if i did it right. If it is good i just have to find y x and i will do it. But i'm sure it is right

Good lord, there is someone who's handwriting is worst than mine.
I simply have absolutely no idea what is contained in that image you posted.
Why not try posting it again using standard text? Or learn to post using LaTeX.