BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
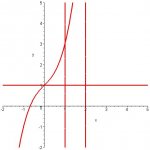
Find volume of the solid formed by revolving the region bounded by the graphs of
y = x3+x+1, y = 1, and x = 1 about the line x = 2, using the disc method, not shells.
Note, you′ll have to solve y = x3+x+1 for x.
y = x3+x+1, y = 1, and x = 1 about the line x = 2, using the disc method, not shells.
Note, you′ll have to solve y = x3+x+1 for x.