You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Can the component of b in a direction with vectors be negative?
- Thread starter burt
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,750
Yes:
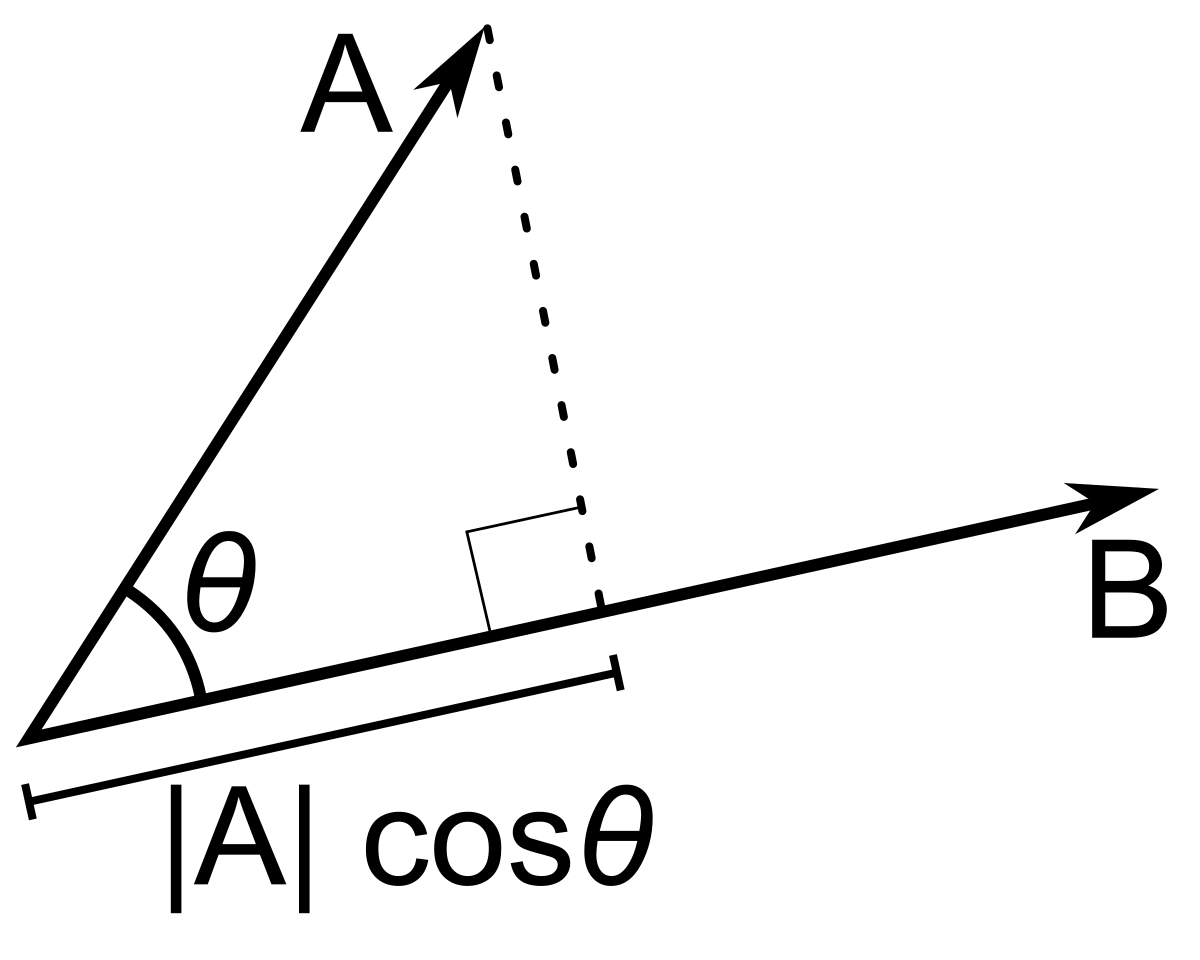
 en.wikipedia.org
en.wikipedia.org
Note that it is not actually a length, but a signed length.

Scalar projection - Wikipedia
The scalar projection is a scalar, equal to the length of the orthogonal projection of [MATH]\mathbf {a}[/MATH] on [MATH]\mathbf {b}[/MATH], with a negative sign if the projection has an opposite direction with respect to [MATH]\mathbf {b}[/MATH].
Note that it is not actually a length, but a signed length.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,989
What is posted seems a bit confused.The scalar projection of b in the a direction is a length. Can this be a negative value?
The idea of projection evolves two vectors. You gave only one.
Look very carefully at the link provided by Prof Peterson.
Yes the direction of \(\displaystyle \vec{b}\) onto \(\displaystyle \vec{a}\), \(\displaystyle \frac{\vec{b}\cdot\vec{a}}{\vec{a}\cdot\vec{a}}\vec{a}\) .
That can be negative if the angle between the vectors is obtuse.
I gave two - the first mentioned is b and the second is a. I'm sorry - I don't know how to do vectors in mathjax so it's not clear.You gave only one.
(But I just looked at yours and now I do - \(\vec{b}\))
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,750
An alternative way to represent vectors is just to use bold: a, b.
