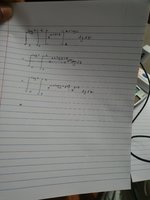You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
calculus-triple integrals
- Thread starter nat190898
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,989
Were you instructed to use base 10 for \(\displaystyle \log(x)~?\)Can someone please solve this and show the steps? Thanks in advance.View attachment 15092
I ask because the trend us usage is quite the other way.
Using \(\displaystyle \log(x)\) as the natural logarithm makes this question easier.
Yes. The question says to take log x as log to base 10 x as an assumption.Were you instructed to use base 10 for \(\displaystyle \log(x)~?\)
I ask because the trend us usage is quite the other way.
Using \(\displaystyle \log(x)\) as the natural logarithm makes this question easier.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
No, sorry, but no one here will show you how to do this step by step. We will however help you do it step by step. Can you show us your attempt at this problem or tell us where you are stuck?
Can you do the inner most integral, the one with respect to dx? Just treat y and z as constant. Please post back with your work.
Can you do the inner most integral, the one with respect to dx? Just treat y and z as constant. Please post back with your work.
This is what I did but when replacing the limits after having integrated wrt x, I end up with a logarithmic function that i do not know how to integrateNo, sorry, but no one here will show you how to do this step by step. We will however help you do it step by step. Can you show us your attempt at this problem or tell us where you are stuck?
Can you do the inner most integral, the one with respect to dx? Just treat y and z as constant. Please post back with your work.
Attachments
Last edited:
Also thank you very much for your responseNo, sorry, but no one here will show you how to do this step by step. We will however help you do it step by step. Can you show us your attempt at this problem or tell us where you are stuck?
Can you do the inner most integral, the one with respect to dx? Just treat y and z as constant. Please post back with your work.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,750
To clarify what you have been told:
The integral as given makes no sense; in order to take the limits of integration as shown, the differentials ought to be reordered, as dz dy dx, so that the inside integral is with respect to z. If the inner integral is with respect to x, then is "uses up" the x, and there can be no x in any of the limits.
As for carrying out the integral, I would start by rewriting the integrand as [MATH]e^x e^y e^z[/MATH], which will make some steps easier.
Also, since calculus works best with natural logs, as soon as it matters you will want to rewrite log(x) as ln(x)/ln(10).
So please confirm what the problem you were given says, and then try again. We'll be glad to help you refine your work, once you are doing a sensible problem.
The integral as given makes no sense; in order to take the limits of integration as shown, the differentials ought to be reordered, as dz dy dx, so that the inside integral is with respect to z. If the inner integral is with respect to x, then is "uses up" the x, and there can be no x in any of the limits.
As for carrying out the integral, I would start by rewriting the integrand as [MATH]e^x e^y e^z[/MATH], which will make some steps easier.
Also, since calculus works best with natural logs, as soon as it matters you will want to rewrite log(x) as ln(x)/ln(10).
So please confirm what the problem you were given says, and then try again. We'll be glad to help you refine your work, once you are doing a sensible problem.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Oops I did not see that x as a limit. SorryCan you do the inner most integral, the one with respect to dx? Just treat y and z as constant. Please post back with your work.
D
Deleted member 4993
Guest
I think it was "hand-writing-po" - should have stated:Check your assumptions list. [math]e^{log(f(x))} \neq log(f(x))[/math], even if we are using [math]log_e \equiv ln[/math]. To demonstrate just let f(x) = 1.
-Dan
[math]e^{log(f(x))} \ = \ \ f(x)[/math]
D
Deleted member 4993
Guest
Back to the corner ...Oops I did not see that x as a limit. Sorry
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,393
Tell him to wait. I'm still there. I don't like it when my corner is full. You won't like me when my corner is full!Back to the corner ...
-Dan