Calculus graphs & dimension areas

[funnytim]

Hey guys!

Some questions in Calculus...

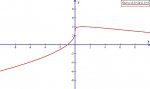
1) Sketch an accurate graph of the curve y = -x[sup:3axjilbw]2/3[/sup:3axjilbw] + 2x[sup:3axjilbw]1/3[/sup:3axjilbw] +3. Find: x-int, y-int, local extrema, points w/ vertical tangent, points of inflection.

So far I have found:
-the y-intersect = 3

y ' = (2/3) (-[cube root x] + x)
so x = 1, -1

Where do I go from here now? I tried to "test" the two points I found above (ie. a number < -1 , a number between -1 and 1, and a number greater than one, and obtained negative, positive, positive, respectively). Not sure if that is right though.


2) A book with cover dimensions 5in * 7in is to be placed symmetrically in a diamond-shaped gift box. What's the smallest possible area of the box? Also show how the answer is minimal.

Other than finding the area of the book (35in[sup:3axjilbw]2[/sup:3axjilbw]) I am not sure how to approach this problem.


Thanks in advance for your assistance!

 

[wjm11]

1) Sketch an accurate graph of the curve y = -x^2/3 + 2x^1/3 +3. Find: x-int, y-int, local extrema, points w/ vertical tangent, points of inflection.

So far I have found:
-the y-intersect = 3

y ' = (2/3) (-[cube root x] + x)
so x = 1, -1

Your y’ is incorrect. What is 2/3 – 1? What is 1/3 – 1?

y = -x^(2/3) + 2x^(1/3) + 3
y' = (-2/3)(x^(-1/3)) + (2/3)(x^(-2/3))

Now set y’ = 0 and solve for x.
Solution: x = 1.

 

[wjm11]

For x intercepts:

0 = -x^(2/3) + 2x^(1/3) + 3
0 = (x^(1/3) – 3)(-x^(1/3) - 1)
Solution: x = -1, 27.


In general, you need to find sufficient points (by building an xy table) to get a rough sketch. This will help you in further analysis and in avoiding mistakes. If you have a graphing calculator, use it.

 

[funnytim]

Your y’ is incorrect

Sorry, I'm not sure what I was doing there. I even wrote down the correct answer on paper

OK, so I was able to draw a rough sketch, more or less accurate when I checked it with my graphing calculator.

However...

To find the points of inflection, I need to take the second derivative, right? I got (hope I'm right this time!)
y '' = 2/9 x [sup:22hwtcdh]-4/3[/sup:22hwtcdh] - 4/9 x [sup:22hwtcdh]-5/3[/sup:22hwtcdh].
But now I'm stuck trying to solve for x. I got as far as factoring out the 2/9...


And just to be sure, there is no vertical tangent in this graph, correct?

Thanks again!

 

[galactus]

Here is the graph, which I am sure you have already graphed.

There is a vertical asymptote at x=0. See it?.

If we factor, we get \(\displaystyle y=\frac{-2(x^{\frac{1}{3}}-1)}{3x^{\frac{2}{3}}}\)

See what makes the denominator 0?. x=0.

 

[soroban]

Hello, funnytim!

2) A book with cover dimensions 5in by 7in
is to be placed symmetrically in a diamond-shaped gift box.
What's the smallest possible area of the box?
Also show how the answer is minimal.

            *
           /|\
          / |:\
         /  |::\
        /  y|:::\
       /    |::::\
      *-----+-----*
     /|     | 2.5 |\
    / |     |     |:\
   /  |     |  3.5|::\ 
  * 7 + - - + - - + - *
   \  |     |     | x/
    \ |     |     | /
     \|     |     |/
      *-----+-----*
       \    5    /
        \       /
         \     /
          \   /
           \ /
            *

\(\displaystyle \text{From the two similar triangles (shaded), we have: }\;\frac{y}{2.5} \,=\,\frac{3.5}{x} \quad\Rightarrow\quad y \,=\,\frac{8.75}{x}\) [1]

\(\displaystyle \text{The area of a rhombus is: }\:A \:=\:\frac{1}{2}\text{( product of the diagonals)}\)

\(\displaystyle \text{The diagonals are: }\:2x+5\,\text{ and }\,2y+7.\)

\(\displaystyle \text{Hence, the area is: }\;A \;=\;(2x+5)(2y+7)\) [2]


Substitute [1] into [2]:

.\(\displaystyle A \;=\;(2x+5)\left(2\left[\tfrac{8.75}{x}\right] + 7 \right) \;=\;14x + 87.5x^{-1} + 70\)


Differentiate, equate to zero, and solve:

. . \(\displaystyle A' \;=\;14 - 87.5x^{-2} \:=\:0 \quad\Rightarrow\quad 14x^2 - 87.5 \:=\:0 \quad\Rightarrow\quad x^2 \:=\:\frac{87.5}{14} \:=\:6.25\)

. . \(\displaystyle \text{Hence: }\:x \,=\,2.5\text{ in.}\)

\(\displaystyle \text{The minimum area is: }\;A \;=\;14(2.5) + \frac{87.5}{2.5} + 70 \;=\;\boxed{ 140\text{ in}^2}\)


\(\displaystyle \text{We have: }\;A'' \:=\:175x^{-3} \:=\:\frac{175}{x^3}\)
\(\displaystyle \text{When }x = 2.5\!:\;\;A'' \:=\:\frac{175}{2.5^3} \:=\:+11.2\)

\(\displaystyle \text{The second derivative is }positive\text{ . . . The function is concave }up\!: \;\cup\)

\(\displaystyle \text{Therefore, }A\text{ is at a minimum at }x = 2.5\)

 

[BigGlenntheHeavy]

galactus, hate to rain on your parade, but there is no vertical asymptote at x = 0, as f(x) is continuous throughout.

 

[funnytim]

Thanks, you guys are awesome!