Calculate the volume of a cube inside an octahedron?

A

Ana.stasia

Junior Member
Joined
Sep 28, 2020
Messages
118
The question is:

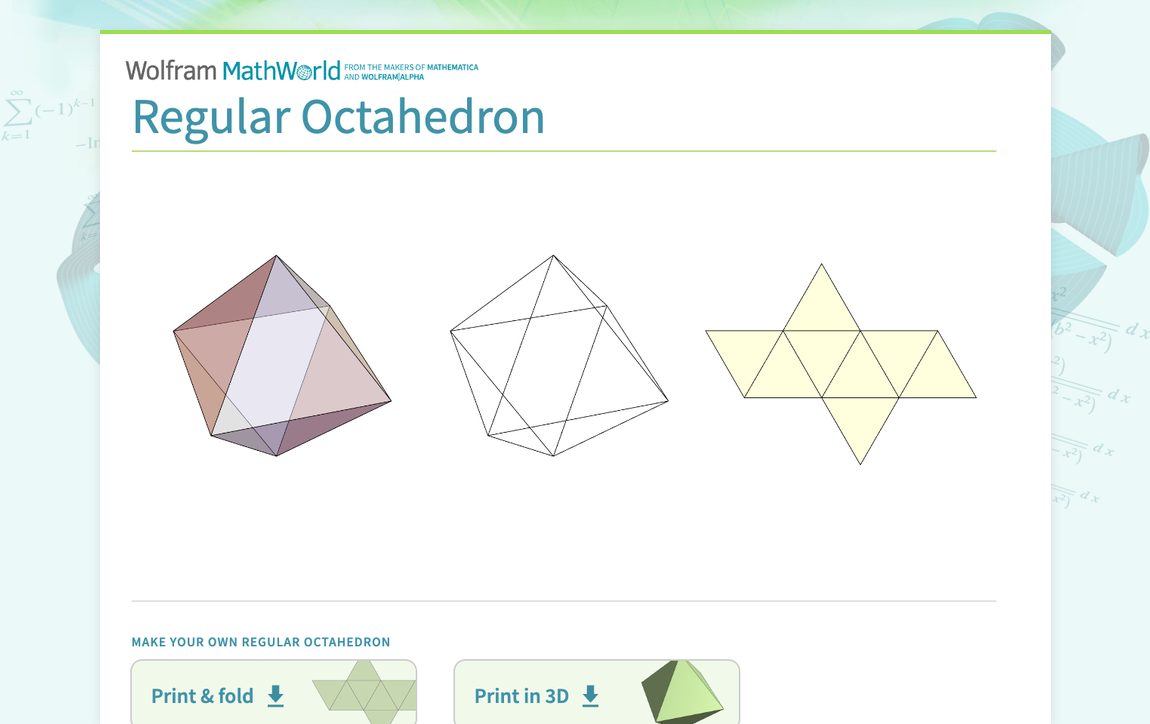
The centers of the sides of the regular octahedron (does the "regular" imply that all edges are equal or just the base ones) are the vertices of a cube. Calculate the volumes of both shapes.

I have tried to draw it, however, it seems my cube is more of a square.

120731550_738691546713866_6713787654108666020_n.jpg

The hint given for this problem is to notice the similarity of the triangles and use them to calculate the edge of the cube. However, I cannot seem to figure out which triangles and how they would relate to the edges of the cube. What am I missing?

Thank you in advance
 
faces of the regular octahedron are equilateral triangles ...

mathworld.wolfram.com

Regular Octahedron -- from Wolfram MathWorld

The regular octahedron, often simply called "the" octahedron, is the Platonic solid with six polyhedron vertices, 12 polyhedron edges, and eight equivalent equilateral triangular faces, denoted 8{3}. It is illustrated above together with a wireframe version and a net that can be used for its...
mathworld.wolfram.com

looks like each vertex of the cube touches each face at its centroid ...

224A785D-9CB4-4754-A9C6-1B4EF4915247.gif
 
ju
skeeter said:
faces of the regular octahedron are equilateral triangles ...

mathworld.wolfram.com

Regular Octahedron -- from Wolfram MathWorld

The regular octahedron, often simply called "the" octahedron, is the Platonic solid with six polyhedron vertices, 12 polyhedron edges, and eight equivalent equilateral triangular faces, denoted 8{3}. It is illustrated above together with a wireframe version and a net that can be used for its...
mathworld.wolfram.com

looks like each vertex of the cube touches each face at its centroid ...

View attachment 22018
Click to expand...

Right, but how can these triangles help me get an edge of the cube?
 
s/3 + s/6 = s/2

The marked line is the projection of the slant height of an equilateral face onto a horizontal plane parallel to the cube’s upper and lower faces. Recall the cube’s vertices are at the centroid of each face, dividing that projection into a 2:1 ratio.

s/3 is a leg of an isosceles right triangle in that horizontal plane. Hypotenuse is [math]\dfrac{s}{3} \cdot \sqrt{2}[/math]
 
So the height that is s/2 is divided by a vertice into two parts. The bottom part is relating to the upper part in a ration 1:2
Which brings us to dividing s/2 by 3 (2+1) and getting s/6. Which multipled by 2, gives us s/3 which is the upper part’s height and s/6 multipling by 1 gives us the bottom part’s height. Then we use that to calculate the edge of the cube.
Did I understand it correctly?
If I did, does the median always divide heights into 2:1 ratio? Even if the triangles do not have all sides equal?
Also does the ratio only relate to height or do sides have something like that too due to a median?
 
(length from triangle vertex to centroid) : (length from centroid to midpoint of the opposite side) is always 2:1

did you not look at the link in post #8 ?
 
skeeter said:
(length from triangle vertex to centroid) : (length from centroid to midpoint of the opposite side) is always 2:1

did you not look at the link in post #8 ?
Click to expand...

I didn't realize it was a link. I just ckecked it out. Now I understand. Thank you.
 
You must log in or register to reply here.
Top