laurence000
New member
- Joined
- Jan 12, 2007
- Messages
- 2
Hi, I'm struggling with sums a lot. The following is what I need to calculate. I could do it "the long way", but how should I approach the problem in order not to calculate it the long way?
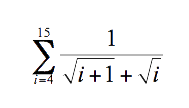
Thank you so much!
Laurence
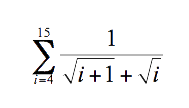
Thank you so much!
Laurence
