Calc 2 problem
- Thread starter sheilaw
- Start date
D
Deleted member 4993
Guest
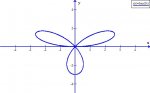
Plot the function in your graphing calculator.sheilaw said:
You'll see there are three symmetric petals of equal size and shape.
So you can find the arc-length of one-half (r = 0 to r = max) petal - then multiply by six(6)
r = 0 at t= 0
At what value of t, you get r = maximum (t[sub:16ru795t]m[/sub:16ru795t])
Then use the arc-length formula and integrate and multiply by 6.
Please show us your work, indicating exactly where you are stuck - so that we know where to begin to help you.
D
Deleted member 4993
Guest
sheilaw said:
To find the limits of integration. set \(\displaystyle 3sin(3{\theta})=0\) and solve for theta.
We find that \(\displaystyle {\theta}=\frac{\pi}{3}\)
the polar arc length formula is \(\displaystyle L=\int_{0}^{\frac{\pi}{3}}\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}d{\theta}\)
This gives the arc length around one petal. So, multiply by 3.
where \(\displaystyle \frac{dr}{d\theta}=9cos(3\theta)\)
And yes, it may not look like it because of the unconstrained scaling, but the petals are all the same in area and arc length.
We find that \(\displaystyle {\theta}=\frac{\pi}{3}\)
the polar arc length formula is \(\displaystyle L=\int_{0}^{\frac{\pi}{3}}\sqrt{r^{2}+\left(\frac{dr}{d\theta}\right)^{2}}d{\theta}\)
This gives the arc length around one petal. So, multiply by 3.
where \(\displaystyle \frac{dr}{d\theta}=9cos(3\theta)\)
And yes, it may not look like it because of the unconstrained scaling, but the petals are all the same in area and arc length.
Attachments
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
galactus, is that the right formula for polar arc length?
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
Thanks, galactus, that's what I thought.
Note: When graphing roses in polar. r = acos(n?) or r = asin(n?), n petals if n is odd and 2n petals if n is even (n?2).
Also note for area and arc length: When n is odd area and/or arc length goes from 0 to ? and when n is even area and/or arc length goes from 0 to 2?. If n is odd and you graph from 0 to 2?, you'll get the same graph if you graphed from 0 to ? as the graph repeats itself, but your measurements will be twice what they should be,
Note: When graphing roses in polar. r = acos(n?) or r = asin(n?), n petals if n is odd and 2n petals if n is even (n?2).
Also note for area and arc length: When n is odd area and/or arc length goes from 0 to ? and when n is even area and/or arc length goes from 0 to 2?. If n is odd and you graph from 0 to 2?, you'll get the same graph if you graphed from 0 to ? as the graph repeats itself, but your measurements will be twice what they should be,
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
Right on, galactus.
After reducing the above integral, I got \(\displaystyle \frac{1}{2}\int_{0}^{6\pi}\sqrt(5+4cos(u))du.\)
I then whipped out my trusty TI-89 and got 20.0473398313,,, (the total arc length) which makes sense as the "radius" of each petal is three, so three twice times three = 18.
Another note: When dealing with arc length (unless the integral is contrived), one in the past had to usually resort to numerical integration (pure drudgery); fortunately now we have TI's or computer programs to do our grunt work.
After reducing the above integral, I got \(\displaystyle \frac{1}{2}\int_{0}^{6\pi}\sqrt(5+4cos(u))du.\)
I then whipped out my trusty TI-89 and got 20.0473398313,,, (the total arc length) which makes sense as the "radius" of each petal is three, so three twice times three = 18.
Another note: When dealing with arc length (unless the integral is contrived), one in the past had to usually resort to numerical integration (pure drudgery); fortunately now we have TI's or computer programs to do our grunt work.
D
Deleted member 4993
Guest
A gas turbine can be approximated through those petals for first approximation of power calculation.galactus said:
There are cross-sections of synthetic fibers - that are tri-lobal, in particular nylon fibers for carpets - whose shapes can be approximated (and behaviour modelled) through these.
Generally, these calculations are reduced to elliptic integrals.
Can some one help me one more question? thank you
An ellipsoid of revolution is obtained by revolving the ellipse x^2/a^2+y^2/b^2=1, around the x-asis. suppose that a>b. Show that the ellipsoid has surface area
A=2piab[b/a+a/(a^2-b^2)^(-1/2)arcsin((a^2-b^2)^(-1/2)/a)]
I found y(x)=b(1-x^2/a^2), y'=-bx/a^2(1-x^2/a^2)^(-1/2)
put it into the surface area formulas
A=2integral(0toa) 2pi b(1-x^2/a^2){1+[ bx/a^2(1-x^2/a^2)^(-1/2)]^2}^1/2 dx
let x=asin(theta) dx=acos(theta)d(theta)
A=4pibintegral(0topi/2) [1-(sin(theta)^2)/a]^(1/2)*{1+b^2sin(theta)^2/a^2(1-sin(theta)^(-1)]^(1/2)*acos(theta)d(theta)
.
.
A=4piabintegral(0topi/2) cos(theta)/a*[a^2+(b^2-a^2)sin(theta)^2]^(1/2)*d(theta)
I tried to solve it, but i dont know to go on
An ellipsoid of revolution is obtained by revolving the ellipse x^2/a^2+y^2/b^2=1, around the x-asis. suppose that a>b. Show that the ellipsoid has surface area
A=2piab[b/a+a/(a^2-b^2)^(-1/2)arcsin((a^2-b^2)^(-1/2)/a)]
I found y(x)=b(1-x^2/a^2), y'=-bx/a^2(1-x^2/a^2)^(-1/2)
put it into the surface area formulas
A=2integral(0toa) 2pi b(1-x^2/a^2){1+[ bx/a^2(1-x^2/a^2)^(-1/2)]^2}^1/2 dx
let x=asin(theta) dx=acos(theta)d(theta)
A=4pibintegral(0topi/2) [1-(sin(theta)^2)/a]^(1/2)*{1+b^2sin(theta)^2/a^2(1-sin(theta)^(-1)]^(1/2)*acos(theta)d(theta)
.
.
A=4piabintegral(0topi/2) cos(theta)/a*[a^2+(b^2-a^2)sin(theta)^2]^(1/2)*d(theta)
I tried to solve it, but i dont know to go on
The distance between the foci is 2c. And \(\displaystyle c=\sqrt{a^{2}-b^{2}}\)
Solve the ellipse equation for y:
\(\displaystyle y=\frac{b}{a}\sqrt{a^{2}-x^{2}}, \;\ \frac{dy}{dx}=\frac{-b}{a}\frac{x}{\sqrt{a^{2}-x^{2}}}, \;\ 1+\left(\frac{dy}{dx}\right)^{2}=\frac{a^{4}-c^{2}x^{2}}{a^{2}(a^{2}-x^{2})}\)
\(\displaystyle S=2(2\pi)\int_{0}^{a}y\sqrt{1+(dy/dx)^{2}}dx=4{\pi}\int_{0}^{a}\frac{b}{a}\sqrt{a^{2}-x^{2}}\frac{\sqrt{a^{4}-c^{2}x^{2}}}{a\sqrt{a^{2}-x^{2}}}dx\)
\(\displaystyle =\frac{4{\pi}b}{a^{2}}\int_{0}^{a}\sqrt{a^{4}-c^{2}x^{2}}dx\)
Let u=cx:
\(\displaystyle \frac{4{\pi}b}{a^{2}c}\int_{0}^{ac}\sqrt{a^{4}-u^{2}}du\)
\(\displaystyle =\frac{4{\pi}b}{a^{2}c}\left[\frac{u}{2}\sqrt{a^{4}-u^{2}}+\frac{a^{4}}{2}sin^{-1}(\frac{u}{a^{2}})\right]_{0}^{ac}\)
\(\displaystyle =\frac{4{\pi}b}{a^{2}c}\left[\frac{1}{2}ac\sqrt{a^{4}-a^{2}c^{2}}+\frac{1}{2}a^{4}sin^{-1}(\frac{c}{a})\right]\)
\(\displaystyle =\boxed{2{\pi}ab\left[\frac{b}{a}+\frac{a}{c}sin^{-1}(\frac{c}{a})\right]}\)
It was difficult to read your post, but is this close to what you need?.
Solve the ellipse equation for y:
\(\displaystyle y=\frac{b}{a}\sqrt{a^{2}-x^{2}}, \;\ \frac{dy}{dx}=\frac{-b}{a}\frac{x}{\sqrt{a^{2}-x^{2}}}, \;\ 1+\left(\frac{dy}{dx}\right)^{2}=\frac{a^{4}-c^{2}x^{2}}{a^{2}(a^{2}-x^{2})}\)
\(\displaystyle S=2(2\pi)\int_{0}^{a}y\sqrt{1+(dy/dx)^{2}}dx=4{\pi}\int_{0}^{a}\frac{b}{a}\sqrt{a^{2}-x^{2}}\frac{\sqrt{a^{4}-c^{2}x^{2}}}{a\sqrt{a^{2}-x^{2}}}dx\)
\(\displaystyle =\frac{4{\pi}b}{a^{2}}\int_{0}^{a}\sqrt{a^{4}-c^{2}x^{2}}dx\)
Let u=cx:
\(\displaystyle \frac{4{\pi}b}{a^{2}c}\int_{0}^{ac}\sqrt{a^{4}-u^{2}}du\)
\(\displaystyle =\frac{4{\pi}b}{a^{2}c}\left[\frac{u}{2}\sqrt{a^{4}-u^{2}}+\frac{a^{4}}{2}sin^{-1}(\frac{u}{a^{2}})\right]_{0}^{ac}\)
\(\displaystyle =\frac{4{\pi}b}{a^{2}c}\left[\frac{1}{2}ac\sqrt{a^{4}-a^{2}c^{2}}+\frac{1}{2}a^{4}sin^{-1}(\frac{c}{a})\right]\)
\(\displaystyle =\boxed{2{\pi}ab\left[\frac{b}{a}+\frac{a}{c}sin^{-1}(\frac{c}{a})\right]}\)
It was difficult to read your post, but is this close to what you need?.
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle I \ get \ S \ = \ \frac{4b\pi}{a^{2}}\int_{0}^{a}\sqrt(a^{4}-a^{2}x^{2}+b^{2}x^{2})dx\)
\(\displaystyle Hence, \ S \ = \ 2ab\pi[\frac{a(arcsin\frac{\sqrt(a^{2}-b^{2})}{a})}{\sqrt(a^{2}-b^{2})}+b]\)
\(\displaystyle Hence, \ S \ = \ 2ab\pi[\frac{a(arcsin\frac{\sqrt(a^{2}-b^{2})}{a})}{\sqrt(a^{2}-b^{2})}+b]\)