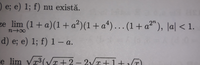Bring these logical expressions to their simplest form

[Mikko]

1. (p⋀q) ⋁∼(∼p⇒q)
2. (p⋁q) ⋁∼(∼p⇒q)
3. (p⇒((∼p⋁q)⇒p))∧q
4. p⋀q((p⋁q)⋀∼q)→q)
5. p⋁∼q⋁∼ p⋁(q⋀∼p)⋁(∼q⋀p)

 

[Mikko]

for example
∼p=>∼∼q
(~p ⇒ ~~q) ⇔ (~p ⇒ q) // bo ~~q ⇔ q

 

[Deleted member 4993]

1. (p⋀q) ⋁∼(∼p⇒q)
2. (p⋁q) ⋁∼(∼p⇒q)
3. (p⇒((∼p⋁q)⇒p))∧q
4. p⋀q((p⋁q)⋀∼q)→q)
5. p⋁∼q⋁∼ p⋁(q⋀∼p)⋁(∼q⋀p)

Please share your work/thoughts about this assignment.

Please follow the rules of posting in this forum, as enunciated at:

READ BEFORE POSTING

 

[Mikko]

2. (p ∨ q) ∨ ~(~p→q)
(p ∨ q) ∨ ~(~~p ∨ q)
(p ∨ q) ∨ ~(p ∨ q)
ok?

 

[pka]

1. (p⋀q) ⋁∼(∼p⇒q)
2. (p⋁q) ⋁∼(∼p⇒q)
3. (p⇒((∼p⋁q)⇒p))∧q
4. p⋀q((p⋁q)⋀∼q)→q)
5. p⋁∼q⋁∼ p⋁(q⋀∼p)⋁(∼q⋀p)

This is a very, very tedious question. You will have to use distribution multiple times.
I will tell you that I would use \(\displaystyle (p \Rightarrow q) \equiv (\neg p \vee q)\), in most of these.