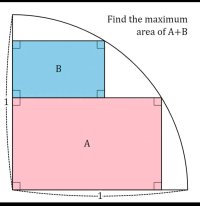
You can solve the problem by symmetry or Lagrange multiplier. But I prefer polar coordinate.
Let [imath]A_1[/imath] be the area of the first rectangle and let [imath]A_2[/imath] be the area of the second rectangle.
[imath]A_1 = x_1y_1[/imath]
[imath]A_2 = x_2y_2[/imath]
[imath]x = r\cos\theta[/imath]
[imath]y = r\sin\theta[/imath]
Then
[imath]A_1 = r^2\cos\theta_1\sin\theta_1[/imath]
[imath]A_2 = r^2\cos\theta_2\sin\theta_2[/imath]
Or
[imath]\displaystyle A_1 = \frac{r^2}{2}\sin2\theta_1[/imath]
[imath]\displaystyle A_2 = \frac{r^2}{2}\sin2\theta_2[/imath]
[imath]\displaystyle A = A_1 + A_2 = \frac{r^2}{2}\sin2\theta_1 + \frac{r^2}{2}\sin2\theta_2 = \frac{r^2}{2}(\sin2\theta_1 + \sin2\theta_2)[/imath]
Now think about it. To get the maximum area, you want [imath]\sin2\theta_1 + \sin2\theta_2[/imath] to be maximum.
Also you must have noticed that because of the symmetry of the two rectangles (they have the same area), [imath]\theta_1 = \theta_2[/imath].
[imath]\displaystyle A = \frac{r^2}{2}(\sin2\theta + \sin2\theta) = r^2\sin2\theta = r^2[/imath]
Finding the angle [imath]\theta[/imath] will help you to find the length of each leg of the rectangle by substituting back in [imath]x[/imath] and [imath]y[/imath].
I will do my calculations again, but this time I will get rid of the overlapping area.
Let [imath]A_1[/imath] be the area of the first rectangle and let [imath]A_2[/imath] be the area of the second rectangle.
[imath]A_1 = x_1y_1[/imath]
[imath]A_2 = x_2y_2 - x_2y_1[/imath]

[imath]x = r\cos\theta[/imath]
[imath]y = r\sin\theta[/imath]
Then
[imath]A_1 = r^2\cos\theta_1\sin\theta_1[/imath]
[imath]A_2 = r^2\cos\theta_2\sin\theta_2 - r^2\cos\theta_2\sin\theta_1[/imath]
Or
[imath]\displaystyle A_1 = \frac{r^2}{2}\sin2\theta_1[/imath]
[imath]\displaystyle A_2 = \frac{r^2}{2}\sin2\theta_2 - r^2\cos\theta_2\sin\theta_1[/imath]
[imath]\displaystyle A = A_1 + A_2 = \frac{r^2}{2}\sin2\theta_1 + \frac{r^2}{2}\sin2\theta_2 - r^2\cos\theta_2\sin\theta_1[/imath]
Now let us assume that the two rectangles are inside a unit circle in the first quadrant.
[imath]\displaystyle A = \frac{1}{2}(\sin2\theta_1 + \sin2\theta_2) - \cos\theta_2\sin\theta_1[/imath]
It is not easy to find by hand when [imath]A[/imath] is a maximum, so you will have to use a CAS, W|A, or any other approximation methods.
I get [imath]\theta_1 \approx 0.553574 \ \ \ \ [/imath] and [imath] \ \ \ \ \theta_2 \approx 1.01722[/imath]
So, the maximum area of the two rectangles when [imath]r = 1[/imath] is:
[imath]\displaystyle A = \frac{1}{2}(\sin2\theta_1 + \sin2\theta_2) - \cos\theta_2\sin\theta_1[/imath]
where [imath]\theta_1[/imath] and [imath]\theta_2[/imath] as mentioned above.
Or in general, the maximum area is:
[imath]\displaystyle A = \frac{r^2}{2}(\sin2\theta_1 + \sin2\theta_2 - 2\cos\theta_2\sin\theta_1)[/imath]