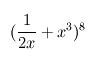binomial theorem help: (1/(2x) + x^3)^8

[alyson]

hey, I'm really struggling on this question i just cant seem to find the right method to get to the answer which is 0.4375

find and simplify the term independent of x in the expansion

\(\displaystyle \left({\frac{1}{2x}}\,+\,x^3\right)^8\)

(i don't know if it'll come up how its meant to so Ive attached a picture of what it should look like)

thanks xx

 

[pka]

Re: binomial theorem help

find and simplify the term independent of x in the expansion
\(\displaystyle ({\frac{1}{2x}}+x^3)^8\)

You want the constant term: \(\displaystyle \left( {2x} \right)^{ - j} \left( {x^3 } \right)^k = c\)
where \(\displaystyle \left\{ \begin{gathered} j + k = 8 \hfill \\ - j + 3k = 0 \hfill \\ \end{gathered} \right.\).
Solve that system.

 

[soroban]

Re: binomial theorem help

Hello, alyson!

\(\displaystyle \text{Find and simplify the term independent of }x\text{ in the expansion of: }\:\left({\frac{1}{2x}}\,+\,x^3\right)^8\)

Did you try to expand it?

I must assume you know the Binomial Theorem.

So you know that: .\(\displaystyle (a+b)^8 \;=\;a^8 + 8a^7b + 28a^6b^2 + 56a^5b^3 + 70a^4b^4 + \hdots\)


\(\displaystyle \text{Then: }\;\left(\frac{1}{2x} + x^3\right)^8 \;=\left(\frac{1}{2x}\right)^8 + 8\left(\frac{1}{2x}\right)^7\left(x^3\right)^1 + 28\left(\frac{1}{2x}\right)^6\left(x^3\right)^2 + 56\left(\frac{1}{2x}\right)^5\left(x^3\right)^3 + \hdots\)

. . . . . . . . . . . . . . \(\displaystyle = \;\frac{1}{256x^8} + 8\left(\frac{1}{128x^7}\right)\left(x^3\right) + 28\left(\frac{1}{64x^6}\right)\left(x^6\right) + 56\left(\frac{1}{32x^5}\right)\left(x^9\right) + \hdots\)

. . . . . . . . . . . . . . \(\displaystyle = \;\frac{1}{256x^8} + \frac{1}{16x^4} + \boxed{\frac{7}{16}} + \frac{7x^4}{4} + \hdots\)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .\(\displaystyle \uparrow\)
. . . . . . . . . . . . . . . . . . . . . . . . . . . There!