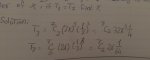The question:
\(\displaystyle \mbox{In the expansion }\, \left(2x\, +\, \dfrac{1}{2}\right)^7,\, \mbox{ find }\, T_3\, \mbox{ and }\, T_7\, \mbox{ according to the decending power}\)
\(\displaystyle x,\, \mbox{ if }\, T_3\, =\, T_7\, \mbox{ Find }\, x.\)
The answer i got:
\(\displaystyle T_3\, =\, {}^7C_2\, (2x)^5\, \left(\dfrac{1}{2}\right)^2\, =\, {}^7C_2\, 32x^5\, \dfrac{1}{4}\)
\(\displaystyle T_7\, =\, {}^2C_6\, (2x)\, \left(\dfrac{1}{2}\right)^6\, =\, {}^7C_6\, 2x\, \dfrac{1}{64}\)
Any help ..
\(\displaystyle \mbox{In the expansion }\, \left(2x\, +\, \dfrac{1}{2}\right)^7,\, \mbox{ find }\, T_3\, \mbox{ and }\, T_7\, \mbox{ according to the decending power}\)
\(\displaystyle x,\, \mbox{ if }\, T_3\, =\, T_7\, \mbox{ Find }\, x.\)
The answer i got:
\(\displaystyle T_3\, =\, {}^7C_2\, (2x)^5\, \left(\dfrac{1}{2}\right)^2\, =\, {}^7C_2\, 32x^5\, \dfrac{1}{4}\)
\(\displaystyle T_7\, =\, {}^2C_6\, (2x)\, \left(\dfrac{1}{2}\right)^6\, =\, {}^7C_6\, 2x\, \dfrac{1}{64}\)
Any help ..
Attachments
Last edited by a moderator: