Beginner Graph Theory Question

I

ifoan

New member
Joined
Oct 19, 2006
Messages
36
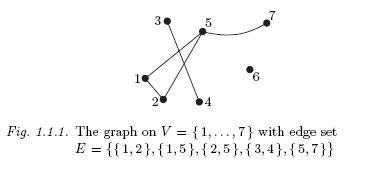
Define V to be the set of all subets of the set
\(\displaystyle \{ 1, 2, 3, 4, 5\}\)
which have cardinality 2. Define E to be the set of all sets \(\displaystyle \{\{v,w\},\{y,z\}\}\) which satisfy
\(\displaystyle \{v,w\}\cap\{y,z\}=0\)

how does the graph look like?

can you construct similar graphs?

How can I approach this problem?

Is this definition of V correct?
\(\displaystyle V := \{(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5), (4,5)\}\)
 
Why did you write them as ordered pairs? It is a bit confusing, unless that is what was asked. Other than that it looks right.

Here is how I interpreted it: The verticies in your set V should be all sets {a,b} with a,b \(\displaystyle \in\) {1,2,3,4,5} and a\(\displaystyle \neq\)b.

For the set of Edges E: Let a, b \(\displaystyle \in\) V. Then a = {x,y} and b={u,v} for some x,y,u,v \(\displaystyle \in\){1,2,3,4,5}. You are looking for all ordered pairs (a,b) = ({x,y}, {u,v}) such that {x,y} and {u,v} are disjoint.

Said another way: If {x,y} is vertex, then scan through the list of verticies in V to find an element {u,v} where x \(\displaystyle \neq\)u, x\(\displaystyle \neq\)v and y\(\displaystyle \neq\)u and y\(\displaystyle \neq\)v. Each time you find one, write down the ordered pair ({x,y},{u,v}). If your graph is directed, note also that ({x,y},{u,v}) is not the same as ({u,v},{x,y}), and that ({u,v},{x,y}) must also be in E.

-Daon
 
Here is another way to think of it. For each two element subset {x,y} there are 3 elements not in it. So there are \(\displaystyle {3 \choose 2} = 3\) edges containing {x,y}.
Daon is correct, the ordered pair notation should not be used.
 
Ok, so far I know I have 5 vertices.

I'm still a little confused as to what the edges are. I thought edges were something like {1,5}, {2,5} and not ({1,5} {3,4})

What I have so far:
untitled-1.jpg


im guessing my graph has to look similar to this:
untitled2.jpg
 
I am an extreme beginner at graph theory. This is what I know so far:

V is the vertices of the Graph.

E is the edges.

V is a "dot" (node) on a graph.

E is a set of two elements on the graph that connect the vertices.

Taking that into consideration:

I'm confused at to how V can be the set of all subsets of the set {1,2,3,4,5} which have cardinality 2. Because \(\displaystyle V := \{\{1,2\}, \{1,3\}, \{1,4\}, \{1,5\}, \{2,3\}, \{2,4\}, \{2,5\}, \{3,4\}, \{3,5\}, \{4,5\}\}\), I'm confused on how these are Vertices because I thought Vertices were one number?

Does this mean my graph in my previous post is wrong? Should I have 10 vertices each labeled {{1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5}}?

Thanks again for all your help! I was forced to take this class. I am an extreme beginner and im having much difficulty
 
another reply!

would we have:

\(\displaystyle V := \{\{1,2\}, \{1,3\}, \{1,4\}, \{1,5\}, \{2,3\}, \{2,4\}, \{2,5\}, \{3,4\}, \{3,5\}, \{4,5\}\}\)

\(\displaystyle E := (\{1,2\} \{3,4\}), (\{1,2\} \{4,5\}), (\{1,2\} \{3,5\}), (\{2,3\} \{1,4\}), (\{2,3\} \{1,5\}), (\{2,3\} \{4,5\}), (\{3,4\} \{1,2\}), (\{3,4\} \{1,5\}), (\{3,4\}, \{2,5\}), (\{4,5\} \{2, 3\}), (\{4,5\} \{1,2\}), (\{4,5\} \{1,3\})\)
 
Come on Ifoan, the graph is not on the set {1,2,3,4,5}.
It is a graph on two element subsets of that set.
There are ten vertices in that graph: {{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5}}.
The vertex {1,2} is connected to each of these vertices {{3,4},{3,5},{4,5}}
As a matter of fact, each vertex is on exactly three edges.
Thus each vertex has order 3 so the are 15 edges.
This is regular connected graph.
 
Yes indeed. Good for you.
BTW: what software are you using for the graphs?
Is the graph bipartite?
 
ms paint

lol

thanks alot of your help. im practically on my own and trying to figure this out with your help and the internets help. i have no lecturer
 
You must log in or register to reply here.
Top