bed of the bridge is not flat but about 6 meters higher in the center than at the tow

[Burqa_@nal_F@g]

Please I need help. I'm currently in pre-cal and I'm new to this forum. IDK who to ask, all of my teachers are gone.

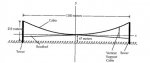
The Golden Gate Bridge in San Francisco is a suspension bridge in which the tow towers are approximately 1280 m apart (see figure).The two main suspension cables are attached to the tops of the towers 213 m above the mean high water level in San Francisco Bay, and the lowest point of each cable is 67 m above the water.

a)The main cables of a suspension bridge hang in the shape of a parabola.Find an equation for the shape of one of the cables of the Golden Gate Bridge.(Assume the origin is placed at the center of the cable, as shown in the figure.)

b) The roadbed of the bridge is not flat but about 6 meters higher in the center than at the towers. (This is partly to allow for downward deflections when the bridge is supporting a load.) If the center of the roadbed is 67 meters above the mean high water level, find an equation for the height of the roadbed at any point. Assume the roadbed also has a parabolic shape, and use the same coordinate system as in part a.
c)Vertical support cables are used to connect the roadbed to the suspension cables. (One is shown in the figure.) Use your equations from a and b to find the length of a vertical support cable that is located 300 m from one of the towers.

I wish i can show a picture of how the bridge looked but idk how to upload pics on here

 

[stapel]

The Golden Gate Bridge in San Francisco is a suspension bridge in which the tow towers are approximately 1280 m apart (see figure). The two main suspension cables are attached to the tops of the towers 213 m above the mean high water level in San Francisco Bay, and the lowest point of each cable is 67 m above the water.

a) The main cables of a suspension bridge hang in the shape of a parabola. Find an equation for the shape of one of the cables of the Golden Gate Bridge.(Assume the origin is placed at the center of the cable, as shown in the figure.)

You are given that the center of the cable is to be placed at the origin. Which point on a parabola does this central (and, in this case, lowest) point represent? What is it called? What then are the values of "h" and "k" in the vertex form of the parabola equation?

You are given that the points (-1280/2, 213-67) and (+1280/2, 213-67) lie on the curve. What other information can you obtain for the parabola equation?

b) The roadbed of the bridge is not flat but about 6 meters higher in the center than at the towers. (This is partly to allow for downward deflections when the bridge is supporting a load.) If the center of the roadbed is 67 meters above the mean high water level, find an equation for the height of the roadbed at any point. Assume the roadbed also has a parabolic shape, and use the same coordinate system as in part a.

This part works exactly the same way.

c)Vertical support cables are used to connect the roadbed to the suspension cables. (One is shown in the figure.) Use your equations from a and b to find the length of a vertical support cable that is located 300 m from one of the towers.

You are given that x = 1280/2 - 300. What did you get when you plugged this into the two y-value equations, and subtracted to find the difference?

Please be complete, showing all of your work and reasoning so far. Thank you!