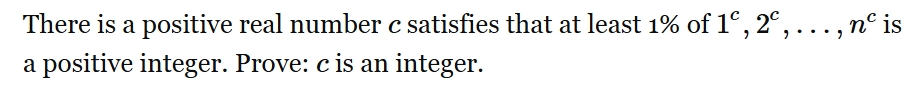at least 1% of 1^c,2^c,...,n^c is a positive integer. Prove: c is an integer.

[astudent]

how to deal with the 1%,thanks.

 

[mmm4444bot]

Posting Guidelines (Summary)

Welcome to our tutoring boards! :) This page summarizes main points from our posting guidelines. As our name implies, we provide math help (primarily to students with homework). We do not generally post immediate answers or step-by-step solutions. We don't do your homework. We prefer to help...

www.freemathhelp.com

 

[Dr.Peterson]

how to deal with the 1%,thanks.

The English in the question is imperfect, and that makes it hard to be sure how to interpret it.

My guess is that it may be intended to say this:

There is a positive real number c such that at least 1% of the numbers [imath]1^c,2^c,\dots,n^c[/imath] are positive integers. Prove that c is an integer.​

Does that sound right to you? (It still isn't clear what n is.) If so, what ideas do you have for solving it?

If it still doesn't make sense, you should ask whoever created this problem what they intended it to mean.

 

[blamocur]

how to deal with the 1%,thanks.

Is this true for any [imath]n[/imath] ?

 

[astudent]

View attachment 38117
The English in the question is imperfect, and that makes it hard to be sure how to interpret it.

My guess is that it may be intended to say this:

There is a positive real number c such that at least 1% of the numbers [imath]1^c,2^c,\dots,n^c[/imath] are positive integers. Prove that c is an integer.​

Does that sound right to you? (It still isn't clear what n is.) If so, what ideas do you have for solving it?

If it still doesn't make sense, you should ask whoever created this problem what they intended it to mean.

yes, and n is any positive integer. And the similar version is 1971 Putnam A6, but without the 1% part.